Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
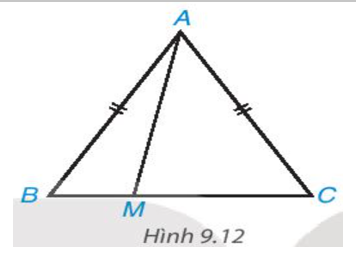
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).

a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
Quảng cáo
Trả lời:
a)
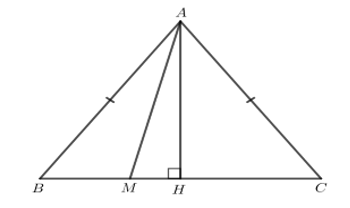
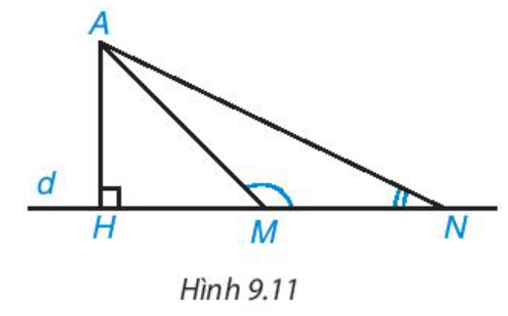
Kẻ AH vuông góc với BC tại H.
M di chuyển trên BC thì AM ≥ AH.
Do đó độ dài AM nhỏ nhất bằng AH.
AM = AH khi M trùng H.
Vậy M là chân đường cao kẻ từ A đến BC thì độ dài AM nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
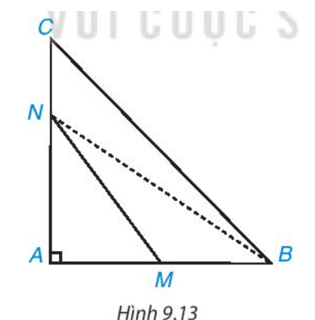
Ta có là góc ngoài tại đỉnh M của tam giác AMN nên
Do đó là góc tù.
có là góc tù nên là tam giác tù.
Do đó cạnh NB đối diện với là cạnh lớn nhất trong .
Khi đó MN < NB (1).
là góc ngoài tại đỉnh N của nên .
Do đó là góc tù.
có là góc tù nên là tam giác tù.
Do đó cạnh BC đối diện với là cạnh lớn nhất trong .
Khi đó NB < BC (2).
Từ (1) và (2) ta có MN < NB < BC.
Vậy MN < BC.
Lời giải
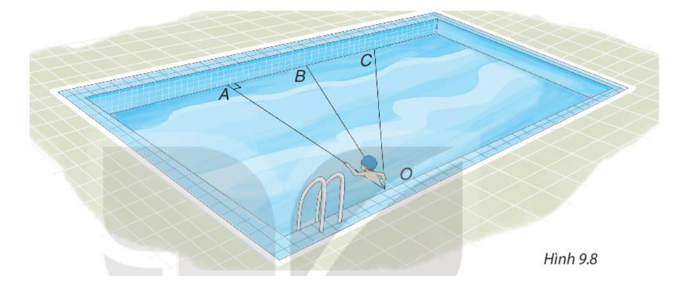
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.
Bài toán đưa về tìm đoạn ngắn nhất trong ba đoạn thẳng OA, OB và OC.
có = 90o nên là góc lớn nhất trong .
Do đó OB > OA (1).
là góc ngoài tại đỉnh B của nên .
Do đó là góc tù.
Xét có là góc tù nên là tam giác tù.
Do đó cạnh OC đối diện với là cạnh lớn nhất trong .
Khi đó OC > OB (2).
Từ (1) và (2) suy ra OC > OB > OA.
Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.