Giải VTH Toán 7 KNTT Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác có đáp án
46 người thi tuần này 4.6 2 K lượt thi 12 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Phúc Hòa (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Tam Hiệp (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Bát Tràng (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Đỗ Ngọc Du (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Chúc Sơn (Hà Nội) có đáp án
Bài tập Tìm điều kiện để số hữu tỉ là một số nguyên lớp 7 (có lời giải)
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Điểm O cách đều ba đỉnh của tam giác ABC khi O là giao điểm của ba đường trung trực của tam giác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
H là giao điểm của ba đường trung trực của tam giác ABC, khi đó H cách đều ba đỉnh của tam giác ABC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
H là giao điểm của ba đường cao của tam giác ABC, khi đó, H là trực tâm của tam giác ABC và vị trí điểm H:
+ Nằm bên trong tam giác ABC khi tam giác này là tam giác nhọn;
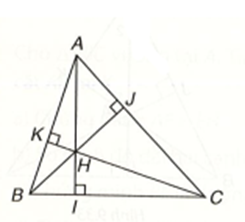
+ Trùng với A khi tam giác ABC là tam giác vuông tại A;
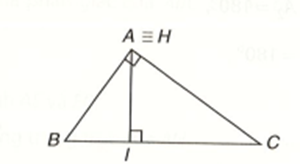
+ Nằm bên ngoài tam giác ABC khi tam giác này là tam giác tù;
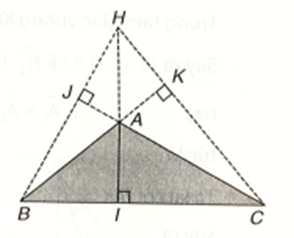
Vậy điểm H có thể nằm ngoài tam giác ABC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
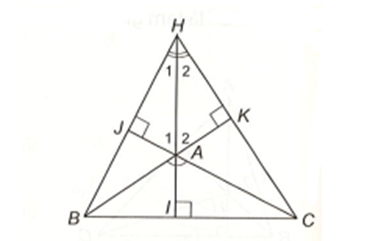
Ta kí hiệu các đường cao AI, BJ, CK, đồng quy tại H và các góc như hình vẽ.
Trong tam giác vuông JHA có \(\widehat {{A_1}} + \widehat {{H_1}} = 90^\circ \).
Trong tam giác vuông KHA có \(\widehat {{H_2}} + \widehat {{A_2}} = 90^\circ \).
Suy ra \(\widehat {{A_1}} + \widehat {{H_1}} + \widehat {{H_2}} + \widehat {{A_2}} = 180^\circ \),
hay \(\left( {\widehat {{H_1}} + \widehat {{H_2}}} \right) + \left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = 180^\circ \), tức là \(\widehat {BHC} + \widehat {JAK} = 180^\circ \).
Ta lại có \(\widehat {JAK} = \widehat {BAC} = 100^\circ \) (đối đỉnh),
suy ra \(\widehat {BHC} = 180^\circ - \widehat {JAK} = 180^\circ - 100^\circ = 80^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
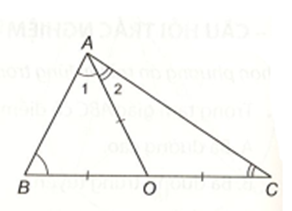
Giả sử O nằm trên cạnh BC thì theo giả thiết, OB = OC nên O là trung điểm của BC.
Từ giả thiết OA = OB = OC nên tam giác OAB cân tại O, tam giác OAC cân tại O.
Vậy \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\), mà \(\widehat A + \widehat B + \widehat C = 180^\circ \), hay \(2\widehat A = 180^\circ \), suy ra \(\widehat A = 180^\circ \) hay tam giác ABC vuông tại A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Để xác định được bán kính của đường viền ngoài, ta lấy ba điểm A, B, C trên đường viền ngoài, rồi dựng điểm đồng quy của ba đường trung trực của tam giác ABC, điểm đồng quy này là tâm của đường tròn đi qua ba điểm A, B, C. Khi đó khoảng cách từ tâm đường tròn tới bất kì một điểm trên đường viền chính là bán kính của đường viền ngoài.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 6/12 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập