Giải VTH Toán 7 KNTT Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
38 người thi tuần này 4.6 1.4 K lượt thi 14 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
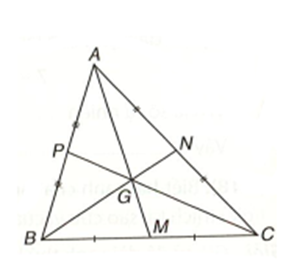
Trong tam giác ABC, các đường trung tuyến AM, BN, CP đồng quy tại điểm G nên G là trọng tâm của tam giác.
Khi đó ta có: \(\frac{{GA}}{{MA}} = \frac{{GB}}{{NB}} = \frac{{GC}}{{PC}} = \frac{2}{3}\). Vậy trong các đáp án đã cho chỉ có đáp án C đúng.
Lời giải
Đáp án đúng là: D
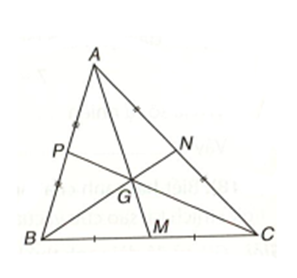
Theo Câu 1, ta có: \(\frac{{GA}}{{MA}} = \frac{{GB}}{{NB}} = \frac{{GC}}{{PC}} = \frac{2}{3}\).
Từ \(\frac{{GA}}{{MA}} = \frac{2}{3}\), suy ra 3GA = 2MA hay 3GA = 2(GA + GM). Suy ra GA = 2GM. Vậy đáp án A đúng.
Tương tự, ta có GB = 2NG, suy ra \(\frac{{NG}}{{GB}} = \frac{1}{2}\). Vậy đáp án B đúng.
Từ \(\frac{{GC}}{{PC}} = \frac{2}{3}\), suy ra 3GC = 2PC hay 3(PC – PG) = 2PC, suy ra PC = 3PG.
Do đó, \(\frac{{PG}}{{PC}} = \frac{1}{3}\). Vậy đáp án C đúng.
Đáp án D sai do \(\frac{{GA}}{{MA}} = \frac{2}{3}\), suy ra \(\frac{{MA}}{{GA}} = \frac{3}{2}\).
Lời giải
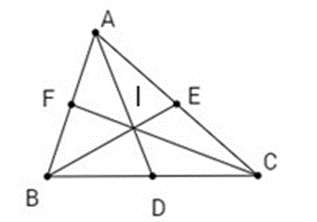
Nếu AD, BE cắt nhau tại I thì CF đi qua I.
Lời giải
Nếu I là điểm chung của ba đường phân giác thì I là giao điểm của ba đường phân giác này và cách đều ba cạnh của tam giác ABC.
Lời giải
Đáp án đúng là: D
I là giao điểm của ba đường phân giác của tam giác nên I cách đều ba cạnh của tam giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.