Chứng minh rằng:
Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
Chứng minh rằng:
Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
Quảng cáo
Trả lời:
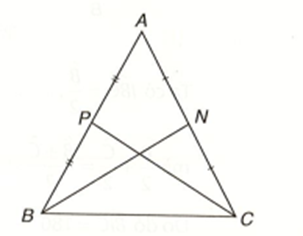
Tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh BN = CP.
Tam giác ABC cân tại A nên AB = AC; \[\widehat {PBC} = \widehat {NCB}\].
Do N, P lần lượt là trung điểm của AC, AB nên BP = \(\frac{1}{2}\)AB, CN = \(\frac{1}{2}\)AC, do đó BP = CN.
Xét hai tam giác BCP và CBN, ta có:
BP = CN; \[\widehat {PBC} = \widehat {NCB}\]; BC chung, do đó ∆BCP = ∆CBN (c.g.c).
Suy ra CP = BN.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
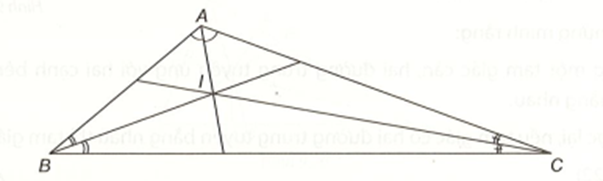
Ta có \(\widehat {IBC} = \frac{{\widehat B}}{2},\,\,\widehat {ICB} = \frac{{\widehat C}}{2}\), \[\widehat {BIC} = 180^\circ - \left( {\frac{{\widehat B}}{2} + \frac{{\widehat C}}{2}} \right)\],
mà \(\frac{{\widehat B}}{2} + \frac{{\widehat C}}{2} = \frac{{\widehat B + \widehat C}}{2} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Do đó \[\widehat {BIC}\] = 180° – 30° = 150°.
Lời giải
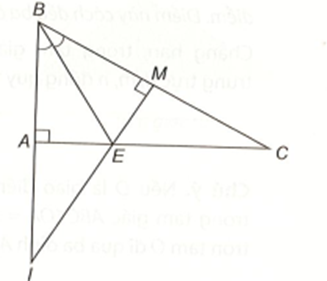
Xét hai tam giác vuông ABE và MBE, ta có:
BE cạnh chụng, \(\widehat {ABE} = \widehat {MBE}\) (BE là tia phân giác góc ABC).
Do đó ∆ABE = ∆MBE (cạnh huyền – góc nhọn).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.