Giải VTH Toán 7 KNTT Bài tập cuối chương 9 có đáp án

38 người thi tuần này 4.6 1.2 K lượt thi 10 câu hỏi

Câu 1

Xem đáp án

Lời giải

$Cho tam giác ABC có \[\widehat {BAC}\] là một góc tù. Lấy điểm D nằm giữa (ảnh 2)$

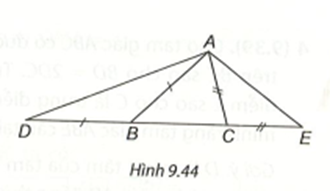
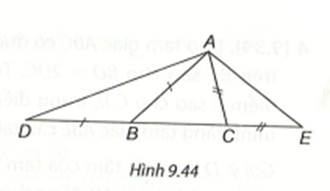
Nối B với E. Trong tam giác BDE, góc BDE tù (do \[\widehat {BAC}\] là góc tù), nên DE < BE.

Trong tam giác BEC, góc BEC tù (cũng do \[\widehat {BAC}\] là góc tù) nên BE < BC.

Suy ra DE < BC.

Câu 2

Xem đáp án

Lời giải

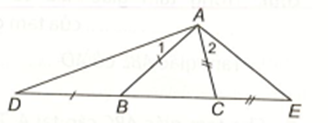
Tam giác ABD cân tại B (AB = BD) và có góc ngoài tại đỉnh B là $\widehat {ABC}$

nên $\widehat D = \widehat {{A_1}} = \frac{1}{2}\widehat {ABC}$.

Tam giác ACE cân tại C (AC = CE) và có góc ngoài tại đỉnh C là $\widehat {ACB}$

nên $\widehat E = \widehat {{A_2}} = \frac{1}{2}\widehat {ACB}$.

Do AB > AC nên $\widehat {ACB} > \widehat {ABC}$, suy ra $\frac{1}{2}\widehat {ACB} > \frac{1}{2}\widehat {ABC}$ hay $\widehat E > \widehat D$.

Câu 3

Xem đáp án

Lời giải

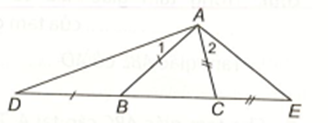
Trong tam giác AED vì \[\widehat {A{\rm{ED}}} > \widehat {A{\rm{D}}E}\] nên AD > AE.

Câu 4

Xem đáp án

Lời giải

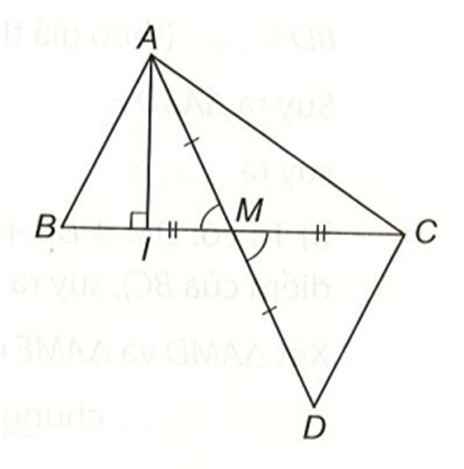
Trong tam giác vuông ABI có AB là cạnh huyền nên AI < AB.

Trong tam giác vuông ACI có AC là cạnh huyền nên AI < AC.

Suy ra 2AI < AB + AC hay AI < \[\frac{1}{2}\](AB + AC).

Câu 5

Xem đáp án

Lời giải

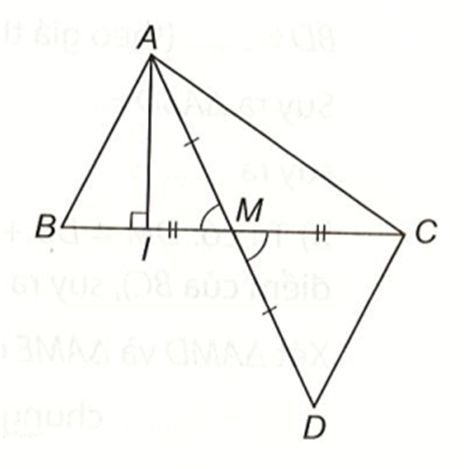
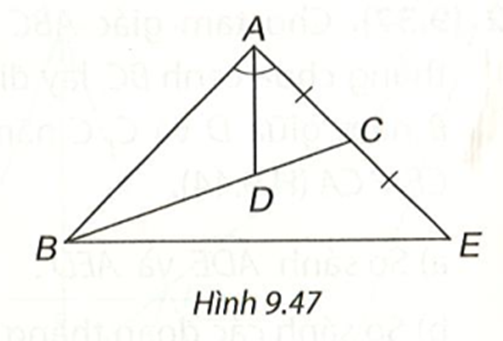
Lấy điểm D sao cho M là trung điểm của AD.

Xét ∆ABM và ∆DCM có: BM = CM; AM = MD; $\widehat {AMB} = \widehat {CMD}$,

do đó ∆ABM = ∆DCM (c.g.c). Suy ra AB = CD.

Trong tam giác ACD, ta có AD < CD + AC hay 2AM < AB + AC.

Suy ra AM < \[\frac{1}{2}\](AB + AC).

Câu 6