Giải SBT Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án

Hướng dẫn giải

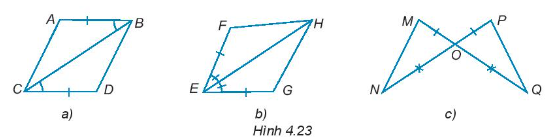
*) Hình a:

Xét ∆ABC và ∆DCB có:  

AB = CD (giả thiết)

BC chung

\(\widehat {ABC} = \widehat {DCB}\) (giả thiết)

Do đó, ∆ABC = ∆DCB (c – g – c).

*) Hình b:

Xét ∆EFH và ∆EGH có:  

EF = EG (giả thiết)

EH chung

\(\widehat {FEH} = \widehat {GEH}\) (giả thiết)

Do đó, ∆EFH = ∆EGH (c – g – c)

*) Hình c:

Xét ∆MON và ∆POQ có:  

MO = PO (giả thiết)

NO = QO (giả thiết)

\(\widehat {MON} = \widehat {POQ}\) (hai góc đối đỉnh)

Do đó, ∆MON = ∆POQ (c – g – c).

Hướng dẫn giải

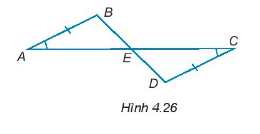
Vì \(\widehat {ABC} = \widehat {DFE}\) nên đỉnh B tương ứng với đỉnh F;

Vì AB = FE mà đỉnh B ứng với đỉnh F thì đỉnh A ứng với đỉnh E.

Suy ra đỉnh C ứng với đỉnh D.

Xét tam giác ABC và tam giác EFD có:

AB = FE;

BC = DF;

 \(\widehat {ABC} = \widehat {DFE}\).

Do đó, ∆ABC = ∆EFD (c – g – c).

Vậy chỉ có đáp án d) đúng.

Hướng dẫn giải

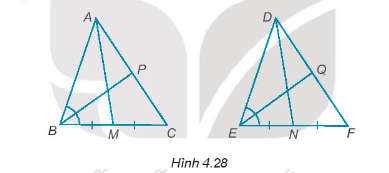
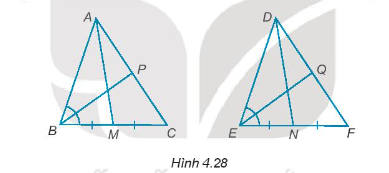
Vì \(\widehat {ABC} = \widehat {PNM}\) nên đỉnh B tương ứng với đỉnh N;

Vì \(\widehat {ACB} = \widehat {NPM}\) nên đỉnh C tương ứng với đỉnh P.

Suy ra đỉnh A tương ứng với đỉnh M.

Xét tam giác ABC và tam giác MNP có:

\(\widehat {ABC} = \widehat {PNM}\)

\(\widehat {ACB} = \widehat {NPM}\)

BC = PN

Do đó, ∆ABC = ∆MNP (g – c – g).

Trong bốn đáp án chỉ có đáp án d chính xác.

Hướng dẫn giải

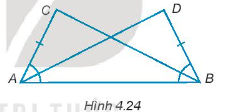
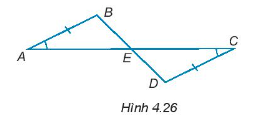
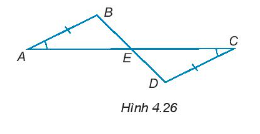
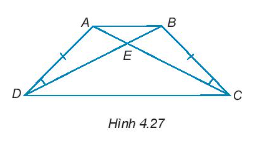
Xét ∆ABC và ∆BAD có:

AC = BD (giả thiết)  

AB chung

\(\widehat {CAB} = \widehat {DBA}\) (giả thiết)

Do đó, ∆ABC = ∆BAD (c – g – c)

Suy ra, BC = AD (hai cạnh tương ứng).

Hướng dẫn giải

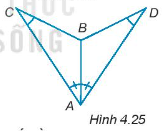
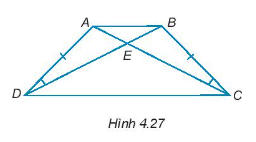
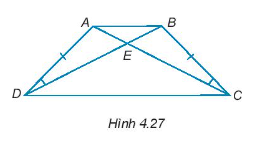
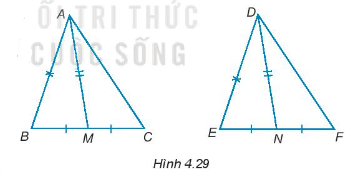
Xét tam giác ABC có:

\[\widehat {ABC} + \widehat {BAC} + \widehat {BCA} = 180^\circ \]

\[\widehat {ABC} = 180^\circ - \widehat {BAC} - \widehat {BCA}\](1)

Xét tam giác ABD có:

\[\widehat {ABD} + \widehat {BAD} + \widehat {BDA} = 180^\circ \]

\[\widehat {ABD} = 180^\circ - \widehat {BAD} - \widehat {BDA}\](2)

Mà \(\widehat {BAC} = \widehat {BAD}\); \(\widehat {BCA} = \widehat {BDA}\) (3)

Từ (1), (2), (3) ta suy ra \(\widehat {ABC} = \widehat {ABD}\).

Xét ∆ABC và ∆ABD có:  

\(\widehat {ABC} = \widehat {ABD}\) (chứng minh trên)

AB chung

\(\widehat {BAC} = \widehat {BAD}\) (giả thiết)

Do đó, ∆ABC = ∆ABD (g – c – g).