Cho hai tam giác ABC và MNP bất kì, thỏa mãn \(\widehat {ABC} = \widehat {PNM}\), \(\widehat {ACB} = \widehat {NPM}\) và BC = PN. Những câu nào dưới đây đúng?
a) ∆ABC = ∆PNM.
b) ∆ABC = ∆NPM.
c) ∆ABC = ∆MPN.
d) ∆ABC = ∆MNP.
Cho hai tam giác ABC và MNP bất kì, thỏa mãn \(\widehat {ABC} = \widehat {PNM}\), \(\widehat {ACB} = \widehat {NPM}\) và BC = PN. Những câu nào dưới đây đúng?
a) ∆ABC = ∆PNM.
b) ∆ABC = ∆NPM.
c) ∆ABC = ∆MPN.
d) ∆ABC = ∆MNP.
Quảng cáo
Trả lời:
Hướng dẫn giải
Vì \(\widehat {ABC} = \widehat {PNM}\) nên đỉnh B tương ứng với đỉnh N;
Vì \(\widehat {ACB} = \widehat {NPM}\) nên đỉnh C tương ứng với đỉnh P.
Suy ra đỉnh A tương ứng với đỉnh M.
Xét tam giác ABC và tam giác MNP có:
\(\widehat {ABC} = \widehat {PNM}\)
\(\widehat {ACB} = \widehat {NPM}\)
BC = PN
Do đó, ∆ABC = ∆MNP (g – c – g).
Trong bốn đáp án chỉ có đáp án d chính xác.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
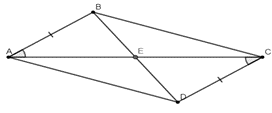
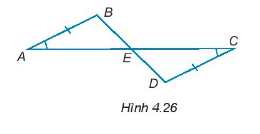
Xét tam giác ABE có:
\[\widehat {BAE} + \widehat {ABE} + \widehat {AEB} = 180^\circ \]
\[\widehat {ABE} = 180^\circ - \widehat {BAE} - \widehat {AEB}\] (1)
Xét tam giác CDE có:
\[\widehat {DCE} + \widehat {DEC} + \widehat {EDC} = 180^\circ \]
\[\widehat {EDC} = 180^\circ - \widehat {DCE} - \widehat {DEC}\] (2)
Mà \(\widehat {BAE} = \widehat {DCE}\) (giả thiết); \(\widehat {AEB} = \widehat {DEC}\) (hai góc đối đỉnh) (3)
Từ (1), (2), (3) ta suy ra \(\widehat {ABE} = \widehat {EDC}\).
Xét ∆ABE và ∆CDE có:
\(\widehat {ABE} = \widehat {EDC}\) (chứng minh trên)
AB = CD (giả thiết)
\(\widehat {BAE} = \widehat {DCE}\) (giả thiết)
Do đó, ∆ABE = ∆CDE (g – c – g).
Suy ra, AE = CE; BE = DE (các cặp cạnh tương ứng)
Vì AE = CE và E nằm giữa A và C nên E là trung điểm của AC;
Vì BE = DE và B nằm giữa D và B nên E là trung điểm của BD.
Lời giải
Hướng dẫn giải:
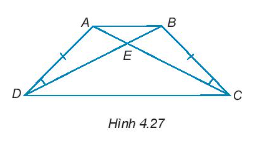
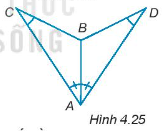
Vì ∆AED = ∆BEC nên AE = BE; ED = EC.
Ta có: AC = AE + EC; BD = BE + ED.
Do đó, AC = BD.
Xét ∆ABD và ∆BAC ta có:
AC = BD (chứng minh trên)
AB chung
AD = CB (giả thiết)
Do đó, ∆ABD = ∆BAC (c – c – c)
Suy ra \(\widehat {ABD} = \widehat {BAC}\) (hai góc tương ứng)
Xét tam giác AEB có:
\(\widehat {ABE} + \widehat {BAE} + \widehat {AEB} = 180^\circ \)
Do đó, \(2\widehat {ABE} = 180^\circ - \widehat {AEB}\) (vì \(\widehat {ABE} = \widehat {BAE}\) do \(\widehat {ABD} = \widehat {BAC}\))
Suy ra \(\widehat {ABE} = \frac{{180^\circ - \widehat {AEB}}}{2}\) (4)
Xét ∆ACD và ∆BDC ta có:
AC = BD (chứng minh trên)
CD chung
AD = CB (giả thiết)
Do đó, ∆ACD = ∆BDC (c – c – c)
Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng)
Xét tam giác DEC có:
\(\widehat {DCE} + \widehat {EDC} + \widehat {DEC} = 180^\circ \)
Do đó, \(2\widehat {EDC} = 180^\circ - \widehat {DEC}\) (vì \(\widehat {EDC} = \widehat {DCE}\) do \(\widehat {ACD} = \widehat {BDC}\))
Suy ra \(\widehat {EDC} = \frac{{180^\circ - \widehat {DEC}}}{2}\) (5)
Lại có, \(\widehat {AEB},\,\,\widehat {DEC}\) là hai góc đối đỉnh nên \(\widehat {AEB} = \widehat {DEC}\) (6)
Từ (4); (5); (6) suy ra \(\widehat {ABE}\) = \(\widehat {EDC}\) hay \(\widehat {ABD} = \widehat {BDC}\).
Mà hai góc này lại ở vị trí so le trong nên AB // CD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.