Giải SBT Toán 7 KNTT Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
45 người thi tuần này 4.6 2 K lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Phúc Hòa (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Tam Hiệp (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Bát Tràng (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Đỗ Ngọc Du (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Chúc Sơn (Hà Nội) có đáp án
Bài tập Tìm điều kiện để số hữu tỉ là một số nguyên lớp 7 (có lời giải)
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
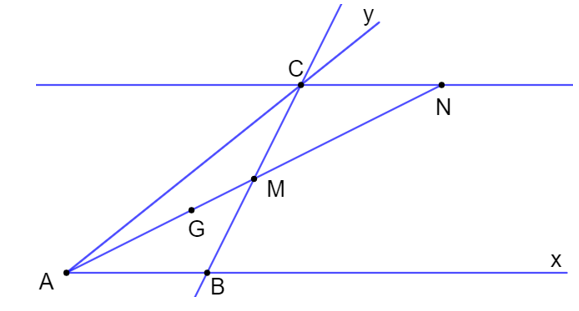
a) Ta có: CN // Ax hay CN // AB
Suy ra (Hai góc so le trong)
Lại có: AN = 2AM nên suy ra AM = NM
Xét hai tam giác ABM và NCM có:
(cmt)
AM = NM (cmt)
(Hai góc đối bằng nhau)
Suy ra ∆ ABM = ∆ NCM (g.c.g)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Ta có: ∆ ABM = ∆ NCM (cmt)
Nên suy ra BM = CM (Hai cạnh tương ứng bằng nhau)
Xét tam giác ABC có BM = CM nên M là trung điểm của BC.
Nên suy ra AM là đường trung tuyến.
Vì G là điểm thuộc AM có .
Hay .
Do đó G là trọng tâm của tam giác ABC (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
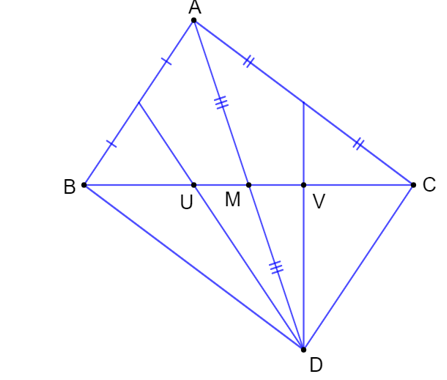
+) Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)
+) Xét tam giác ABD có U là giao của 2 đường trung tuyến BM và DE nên U là trọng tâm tam giác ABD
Vậy áp dụng định lí 1 ta có:
Suy ra (2)
Từ đó ta có: (3)
+) Xét tam giác ACD có V là giao của 2 đường trung tuyến CM và DF nên V là trọng tâm tam giác AVD
Vậy áp dụng định lí 1 ta có:
Suy ra (4)
Từ đó ta có: (5)
Từ (1), (3), (5) ta có:
(6)
Từ (1), (2), (4), (6) ta có: (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
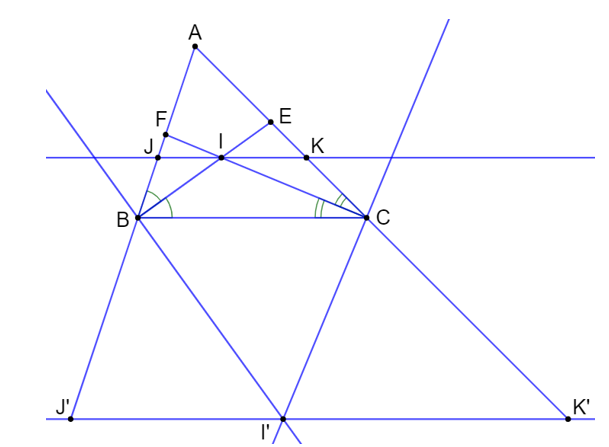
a) Xét tam giác BFC có BI là đường phân giác nên ta có:
hay (5)
Lại có do JI // BC nên ta suy ra được: (hai góc so le trong)
Vậy suy ra . Từ đó ta suy tam tam giác JIB cân tại J.
Suy ra JI = BJ (1)
Tương tự ta chứng minh được tam giác KIC cân tại I.
Suy ra KI = CK (2)
Từ (1) và (2) suy ra: JK = JI + IK = BJ + CK (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Vì BI’ vuông góc với BI nên (3)
Và (4)
Từ (3), (4) và (5) suy ra .
Vậy suy ra BI’ là tia phân giác của góc tạo bởi BC và BJ’.
Chứng minh tương tự ta suy ra CI’ là tia phân giác của góc tạo bởi CB và CK’.
Chứng minh tương tự câu a) ta dễ dàng suy ra được tam giác J’BI’ cân tại J’ và tam giác K’CI’ cân tại K’.
Vậy suy ra J’B = J’I’ và K’C = K’I’.
Vậy ta có: J’K’ = J’I’ + I’K’ = J’B + K’C (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi Ax là tia đối của tia AB thì ba góc BAD, DAC, CAx có cùng số đo 60º.
Hạ EH ⏊ Bx, EI ⏊ AD, EK ⏊ BC.
Ta có: Vì BE là phân giác góc ABC nên suy ra EH = EK (Áp dụng định lí 2).
Vì AE là phân giác góc DAx nên suy ra EH = EI (Áp dụng định lí 2).
Suy ra EK = EI hay E nằm trên tia phân giác của ADC.
Vậy suy ra DE là đường phân giác của góc ADC (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 1/7 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập