Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
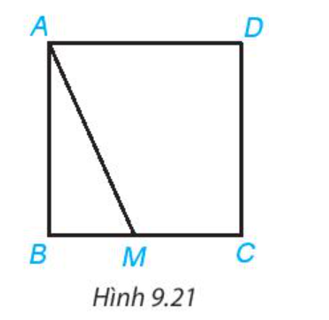
Nếu M trung với B hoặc D thì độ dài AM chính là độ dài hình cạnh hình vuông ABCD.
Với M khác B và thuộc cạnh BC thì AM, AB lần lượt là đường xiên, đường vuông góc kẻ từ A đến BC.
Do đó AM > AB.
Tương tự, khi M khác D và thuộc cạnh CD thì AM > AD.
Mà AB = AD là độ dài cạnh của hình vuông ABCD.
Khi đó AM luôn lớn hơn độ dài cạnh của hình vuông ABCD.
Vậy nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó.
Lời giải
Ta có 2,5 + 3,4 = 5,9 < 6, độ dài ba đoạn thẳng 2,5 cm; 3,4 cm và 6 cm không thỏa mãn một bất đẳng thức tam giác nên không phải độ dài ba cạnh của một tam giác.
Do đó không có tam giác nào có độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm.
Lời giải
Trường hợp 1: bộ ba cạnh của tam giác là 2cm; 2cm; 5cm.
Ta thấy 2 + 2 = 4 < 5 nên bộ ba số này không tạo thành một tam giác.
Trường hợp 2: bộ ba cạnh của tam giác là 5cm, 5cm, 2cm.
Ta thấy 5 + 5 = 10 > 2; 5 + 2 = 7 > 5 nên bộ ba số nfy tạo thành một tam giác với cạnh đáy là 2cm và hai cạnh bên là 5cm.
Chu vi tam giác đó là:
5 + 5 + 2 = 12 (cm)
Lời giải
Gọi độ dài cạnh còn lại của tam giác là x cm (x > 0).
Áp dụng bất đẳng thức tam giác ta có:
7 - 2 < x < 7 + 2 hay 5 < x < 9.
Mà x là một số tự nhiên lẻ nên x = 7.
Vậy độ dài cạnh còn lại của tam giác bằng 7 cm.
Lời giải
Gọi độ dài cạnh còn lại của tam giác là c (cm, c > 0).
Chu vi của tam giác là a + b + c.
Khi đó áp dụng bất đẳng thức tam giác ta có c < a + b và a < b + c.
Do c < a + b nên a + b + c < a + b + a + b hay a + b + c < 2(a + b).
Do a < b + c nên a + a < a + b + c hay 2a < a + b + c.
Vậy chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.