Câu hỏi:
12/07/2024 4,916
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Câu hỏi trong đề: Bài tập Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi độ dài cạnh còn lại của tam giác là c (cm, c > 0).
Chu vi của tam giác là a + b + c.
Khi đó áp dụng bất đẳng thức tam giác ta có c < a + b và a < b + c.
Do c < a + b nên a + b + c < a + b + a + b hay a + b + c < 2(a + b).
Do a < b + c nên a + a < a + b + c hay 2a < a + b + c.
Vậy chu vi của tam giác đó lớn hơn 2a và nhỏ hơn 2(a + b).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
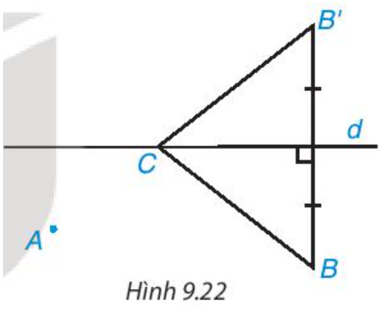
Gọi B’ là điểm sao cho d là đường trung trực của đoạn thẳng BB’.
Vì C nằm trên đường trung trực của BB’ nên C cách đều hai đầu mút B và B’ nên CB = CB’.
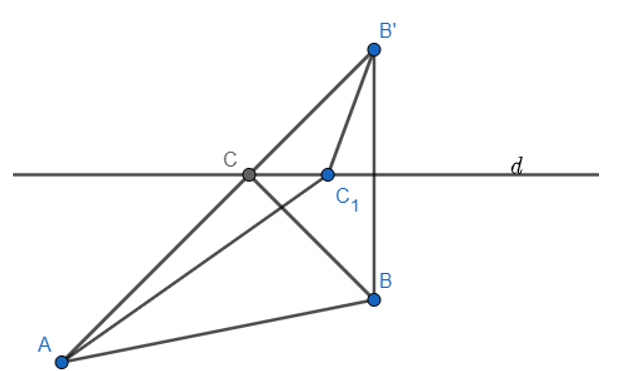
Gọi B’ là điểm sao cho d là đường trung trực của BB’.
Do d là đường trung trực của BB’ và C thuộc d nên CB’ = CB.
Khi đó AC + CB = AC + CB’ ≥ AB’.
Khi đó giá trị nhỏ nhất của AC + CB’ bằng AB’.
AC + CB’ = AB’ khi C nằm giữa A và B’.
Vậy C là giao điểm của d và AB’ với B’ là điểm sao cho d là đường trung trực của BB’.
Lời giải
Trường hợp 1: bộ ba cạnh của tam giác là 2cm; 2cm; 5cm.
Ta thấy 2 + 2 = 4 < 5 nên bộ ba số này không tạo thành một tam giác.
Trường hợp 2: bộ ba cạnh của tam giác là 5cm, 5cm, 2cm.
Ta thấy 5 + 5 = 10 > 2; 5 + 2 = 7 > 5 nên bộ ba số nfy tạo thành một tam giác với cạnh đáy là 2cm và hai cạnh bên là 5cm.
Chu vi tam giác đó là:
5 + 5 + 2 = 12 (cm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2