Giải VTH Toán 7 KNTT Bài 32. Quan hệ giữa đường vuông góc và đường xiên có đáp án
64 người thi tuần này 4.6 1.4 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
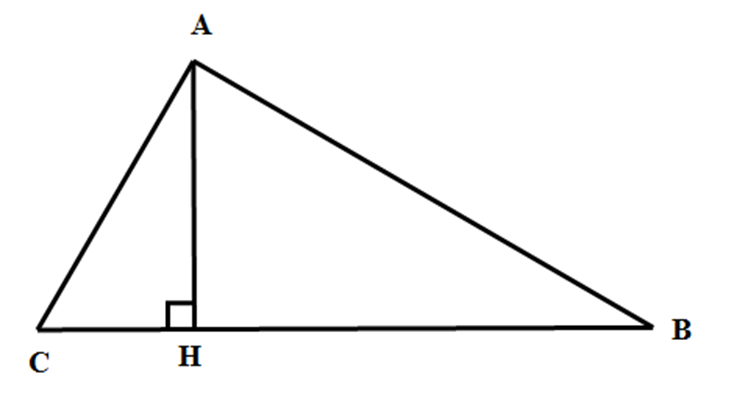
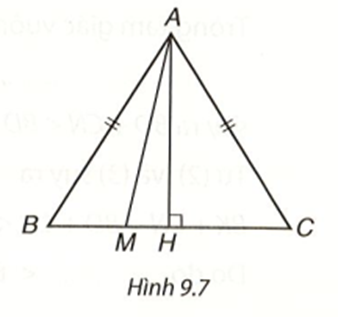
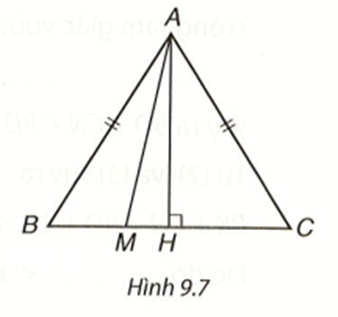
Tam giác ABC có đường cao AH nên AH là đường vuông góc kẻ từ A đến BC và AB, AC là các đường xiên kẻ từ A kến BC.
Do đó, AB > Ah, AC > AH, vậy đáp án A, B sai và đáp án C đúng.
Ta có \(\widehat B < \widehat C\) thì AC < AB nên đáp án D sai.
Lời giải
Đáp án đúng là: D
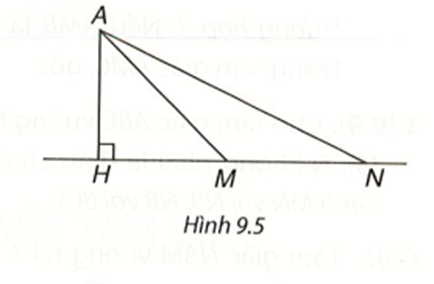
Do AH vuông góc với đường thẳng MN tại H nên AH là đường vuông góc kẻ từ A đến MN và AM, AN là các đường xiên kẻ từ A đến MN.
Suy ra AH < AM, AH < AN. Vậy đáp án D đúng.
Lời giải
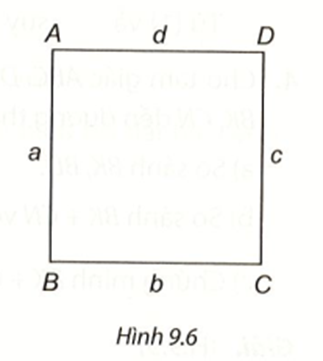
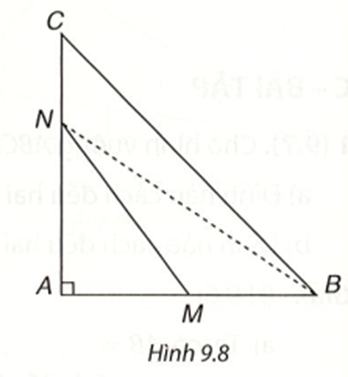
Ta có AB = AD và CB = CD nên hai đỉnh B và D cách đều hai điểm A và C.
Lời giải
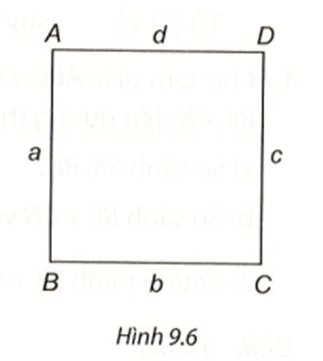
• Ta có CB ⊥ AB nên CB là khoảng cách từ C đến AB. Tương tự do CD ⊥ AD nên CD là khoảng cách từ C đến AD. Mặt khác ta có CB = CD. Vậy C là một điểm cách đều hai đường thẳng AB và AD.
• Vì điểm A nằm trên hai đường thẳng AB và AD nên khoảng cách từ A đến hai đường thẳng ấy bằng nhau. Vậy A cũng là một điểm cách đều hai đường thẳng AB và AD.Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.