Giải VTH Toán 7 KNTT Bài tập ôn tập cuối năm Hình học và Đo lường có đáp án
39 người thi tuần này 4.6 1.7 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
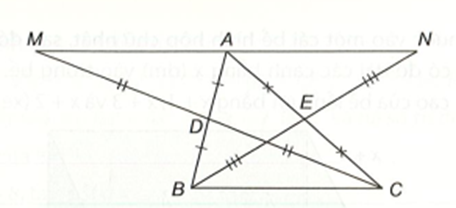
∆ADM và ∆BDC có:
AD = DB (do D là trung điểm của AB)
\[\widehat {A{\rm{D}}M} = \widehat {B{\rm{D}}C}\] (hai góc đối đỉnh)
DM = DC (giả thiết)
Nên ∆ADM = ∆BDC (c.g.c).
Suy ra AM = BC (hai cạnh tương ứng) và \[\widehat {MAD} = \widehat {CBD}\] (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AM // BC (dấu hiệu nhận biết hai đường thẳng song song).
Lời giải
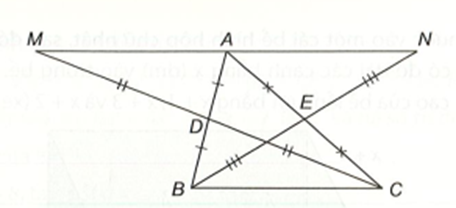
∆AEN và ∆CEB có:
AE = CE (E là trung điểm của AC)
\[\widehat {A{\rm{E}}N} = \widehat {CEB}\] (hai góc đối đỉnh)
EN = EB (theo giả thiết)
Nên ∆AEN = ∆CEB (c.g.c).
Suy ra \[\widehat {E{\rm{A}}N} = \widehat {ECB}\] (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AN // BC (dấu hiệu nhận biết hai đường thẳng song song).
Lời giải
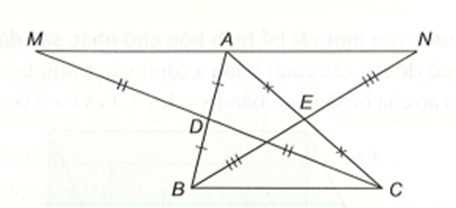
Ta có AM // BC (chứng minh trên),
AN // BC (chứng minh trên) nên AM và AN trùng nhau (theo tiên đề Euclid).
Từ đó suy ra ba điểm M, A, N thẳng hàng.
Ta lại có AM = BC (chứng minh trên), AN = BC (chứng minh trên – do ∆AEN = ∆CEB),
do đó AM = AN.
Từ đó suy ra A là trung điểm của đoạn MN.
Lời giải
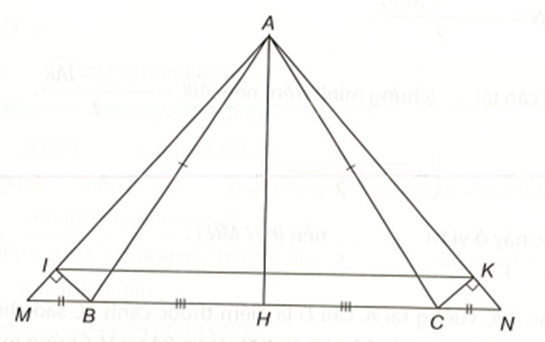
∆ABC cân tại A (giả thiết)
Mà AH là trung tuyến (H là trung điểm của BC).
Nên AH là đường cao của ∆ABC (tính chất tam giác cân).
Vậy AH ⊥ BC.
Lời giải
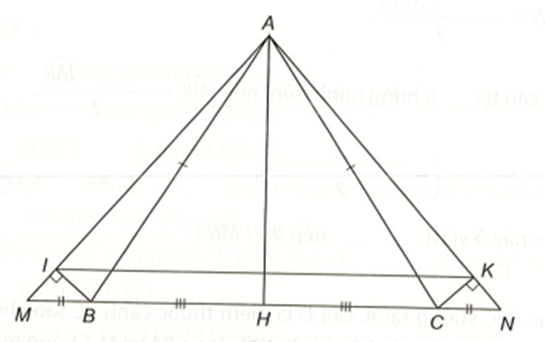
Ta có \[\widehat {ABM} + \widehat {ABC} = 180^\circ \] (hai góc kề bù),
\[\widehat {ACN} + \widehat {ACB} = 180^\circ \] (hai góc kề bù).
Mà \[\widehat {ABC} = \widehat {ACB}\] nên \[\widehat {ABM} = \widehat {ACN}\].
∆ABM và ∆ACN có:
AB = AC (∆ABC cân tại đỉnh A).
\[\widehat {ABM} = \widehat {ACN}\] (chứng minh trên).
BM = CN (theo giả thiết).
Nên ∆ABM = ∆ACN (c.g.c).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.