Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Phúc Hòa (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Tam Hiệp (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Bát Tràng (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Đỗ Ngọc Du (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 7 năm 2025-2026 THCS Chúc Sơn (Hà Nội) có đáp án
Bài tập Tìm điều kiện để số hữu tỉ là một số nguyên lớp 7 (có lời giải)
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 7 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
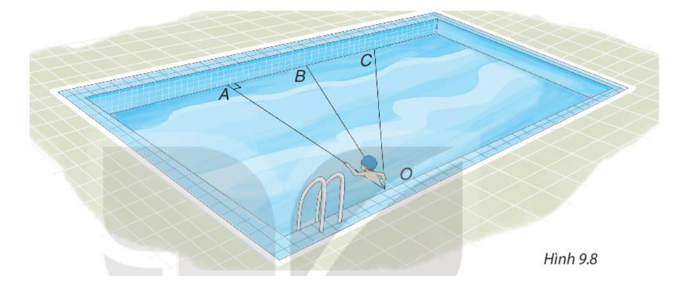
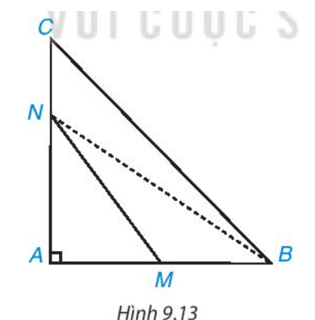
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.
Bài toán đưa về tìm đoạn ngắn nhất trong ba đoạn thẳng OA, OB và OC.
có = 90o nên là góc lớn nhất trong .
Do đó OB > OA (1).
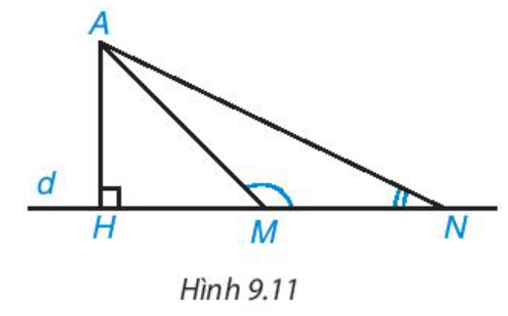
là góc ngoài tại đỉnh B của nên .
Do đó là góc tù.
Xét có là góc tù nên là tam giác tù.
Do đó cạnh OC đối diện với là cạnh lớn nhất trong .
Khi đó OC > OB (2).
Từ (1) và (2) suy ra OC > OB > OA.
Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
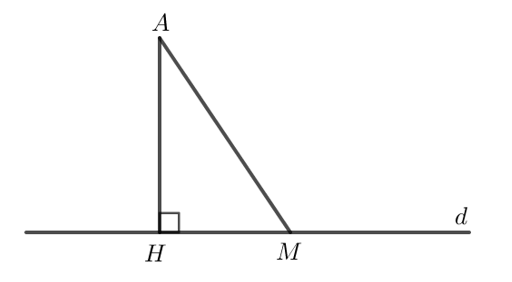
b) Do AH d nên = 90o.
Nên tam giác AHM là tam giác vuông.
Suy ra cạnh huyền AM là cạnh huyền.
Mà trong tam giác vuông cạnh huyền là cạnh dài nhất nên AM > AH.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
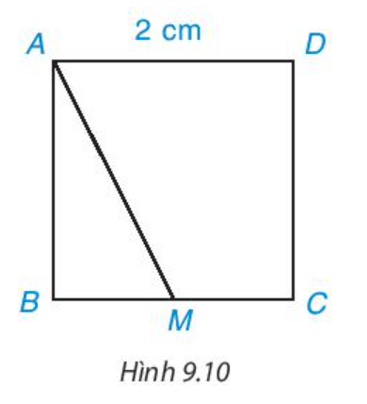
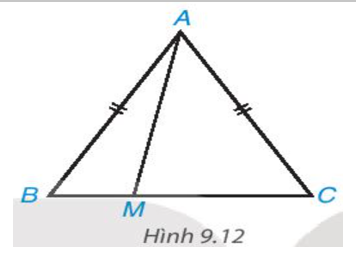
a) Đường vuông góc kẻ từ A đến đường thẳng BC là AB.
Đường xiên kẻ từ A đến đường thẳng BC là AM.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AB là đường ngắn nhất.
Do đó AM > AB.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
c) Đường vuông góc kẻ từ điểm C đến đường thẳng AB là CB.
Khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn BC.
Do ABCD là hình vuông nên BC vuông góc với AB tại B. Do đó, BC = AD = 2 cm.
Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 9/15 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập