Giải SBT Toán 7 KNTT Ôn tập chương 10 có đáp án
77 người thi tuần này 4.6 1.3 K lượt thi 15 câu hỏi
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
20.4 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
7.2 K lượt thi
30 câu hỏi
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
15 K lượt thi
15 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
15.7 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
5.6 K lượt thi
23 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
15.4 K lượt thi
29 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
5.6 K lượt thi
21 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
15 K lượt thi
29 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
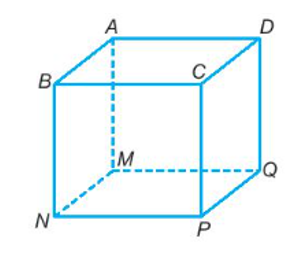
Hình hộp chữ nhật ABCD.MNPQ có 6 mặt là: ABCD, MNPQ, AMNB, BNPC, CPQD, DQMA.
Chọn đáp án B.
Lời giải
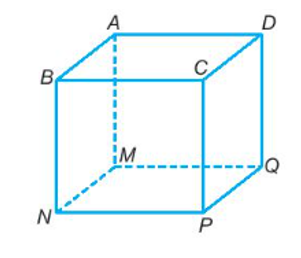
Hình lập phương ABCD.MNPQ có 8 đỉnh là: A, B, C, D, M, N, P, Q.
Chọn đáp án D.
Lời giải
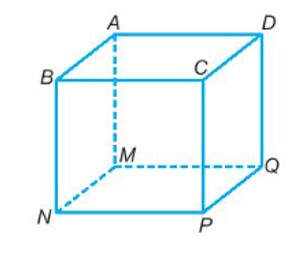
Hình hộp chữ nhật ABCD.MNPQ có 12 cạnh là:
AB, BC, CD, DA, MN, NP, PQ, QM, AM, BN, CP, DQ.
Chọn đáp án B.
Lời giải
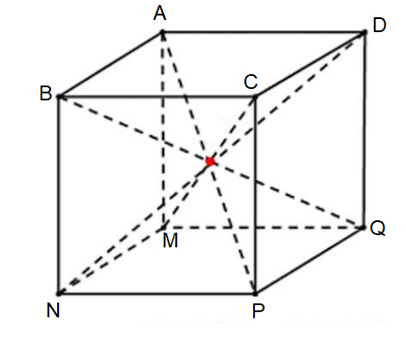
Quan sát hình vẽ, ta thấy hình lập phương ABCD.MNPQ có 4 đường chéo là: AP, BQ, CM, DN.
Chọn đáp án C.
Câu 5
Mặt bên của hình lăng trụ đứng tam giác là:
A. Hình tam giác
B. Hình thoi
C. Hình chữ nhật
D. Hình lục giác đều
Mặt bên của hình lăng trụ đứng tam giác là:
A. Hình tam giác
B. Hình thoi
C. Hình chữ nhật
D. Hình lục giác đều
Lời giải
Mặ bên của lăng trụ đứng tam giác ABC.DEF là hình chữ nhật ABED.
Chọn đáp án C.
Câu 6
Các cạnh bên của hình lăng trụ đứng:
A. song song và không bằng nhau
B. cắt nhau
C. vuông góc với nhau
D. song song và bằng nhau
Các cạnh bên của hình lăng trụ đứng:
A. song song và không bằng nhau
B. cắt nhau
C. vuông góc với nhau
D. song song và bằng nhau
Lời giải
Quan sát hình lăng trụ đứng ABC.DEF, ta thấy:
Các cạnh bên của lăng trụ đứng ABC.DEF là AD, BE, CF. Các cạnh trên song song với nhau và bằng nhau.
Chọn đáp án D.
Lời giải
Thể tích hình lập phương có cạnh dài 5 cm là:
V = 53 = 125 (cm3)
Vậy thể tích hình lập phương có cạnh dài 5 cm là 125 cm3.
Chọn đáp án C.
Câu 8
Hình lăng trụ đứng tam giác có đáy là tam giác đều cạnh 3 cm, chiều cao hình lăng trụ bằng 10 cm. Diện tích xung quanh của hình lăng trụ đó là:
A. 30 cm2
B. 90 cm2
C. 90 cm3
D. 13 cm2
Hình lăng trụ đứng tam giác có đáy là tam giác đều cạnh 3 cm, chiều cao hình lăng trụ bằng 10 cm. Diện tích xung quanh của hình lăng trụ đó là:
A. 30 cm2
B. 90 cm2
C. 90 cm3
D. 13 cm2
Lời giải
Chu vi mặt đáy có dạng tam giác đều có cạnh bằng 3 cm là:
C = 3 . 3 = 9 (cm)
Diện tích xung quanh của hình lăng trụ đứng có đáy là tam giác đều là:
Sxq = C . h = 9 . 10 = 90 (cm2)
Vậy diện tích xung quanh của hình lăng trụ là 90 cm2.
Chọn đáp án B.
Câu 9
Một hình lăng trụ đứng, đáy là hình thang, chiều cao hình lăng trụ bằng 5 cm. Thể tích của hình lăng trụ nói trên bằng 50 cm3. Diện tích một đáy lăng trụ bằng:
A. 10 cm2
B. 250 cm2
C. 55 cm2
D. 10 cm3
Một hình lăng trụ đứng, đáy là hình thang, chiều cao hình lăng trụ bằng 5 cm. Thể tích của hình lăng trụ nói trên bằng 50 cm3. Diện tích một đáy lăng trụ bằng:
A. 10 cm2
B. 250 cm2
C. 55 cm2
D. 10 cm3
Lời giải
Diện tích một đáy lăng trụ bằng:
S = V : h = 50 : 5 = 10 (cm2).
Vậy diện tích một đáy lăng trụ bằng 10 cm2.
Chọn đáp án A.
Câu 10
Một hình hộp chữ nhật có đáy là hình vuông có thể tích 150 cm3. Chiều cao của hình hộp bằng 6 cm. Chu vi đáy của hình hộp chữ nhật là:
A. 25 cm
B. 20 cm2
C. 20 cm
D. 900 cm
Một hình hộp chữ nhật có đáy là hình vuông có thể tích 150 cm3. Chiều cao của hình hộp bằng 6 cm. Chu vi đáy của hình hộp chữ nhật là:
A. 25 cm
B. 20 cm2
C. 20 cm
D. 900 cm
Lời giải
Hình chữ nhật trên có đáy là hình vuông.
Diện tích một đáy của hình hộp chữ nhật đó là:
S = V : h = 150 : 6 = 25 (cm2).
Gọi a (cm) là độ dài cạnh của mặt đáy có dạng hình vuông.
Khi đó diện tích của hình vuông là: a2 (cm2).
Ta có: a2 = 25 nên suy ra a = 5 (cm).
Khi đó, cạnh của mặt đáy có dạng hình vuông là 5 cm.
Chu vi đáy của hình hộp chữ nhật là:
C = 4 . 5 = 20 (cm).
Vậy chu vi đáy của hình hộp chữ nhật là 20 cm.
Chọn đáp án C.
Câu 11
Cho hình hộp chữ nhật có kích thước như trên Hình 10.13. Tính thể tích, diện tích xung quanh của hình hộp chữ nhật.
Cho hình hộp chữ nhật có kích thước như trên Hình 10.13. Tính thể tích, diện tích xung quanh của hình hộp chữ nhật.
Lời giải
Thể tích của hình hộp chữ nhật là:
V = 5 . 8 . 6 = 240 (cm3)
Chu vi mặt đáy của hình hộp chữ nhật là:
C = 2 . (8 + 5) = 26 (cm)
Diện tích xung quanh của hình hộp chữ nhật đó là:
S = C . h = 26 . 6 = 156 (cm2)
Vậy diện tích xung quanh của hình hộp chữ nhật đó là 156 cm2.
Câu 12
Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m và chiều cao 1,8 m. Người thợ cần bao nhiêu kilôgam sơn để đủ sơn toàn bộ mặt ngoài của chiếc thùng đó, biết rằng mỗi kilôgam sơn có thể sơn được 5 m2 mặt thùng.
Lời giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
C = 2 . (3 + 2) = 10 (m)
Diện tích xung quanh của thùng đựng hàng đó là:
Sxq = C . h = 10 . 1,8 = 18 (m2)
Diện tích mặt đáy của hình hộp chữ nhật là:
Sđáy = 3 . 2 = 6 (m2)
Diện tích hai đáy của thùng đựng hàng là:
S2đáy = 6 . 2 = 12 (m2)
Diện tích toàn phần của thùng đựng hàng đó là:
18 + 12 = 30 (m2)
Số kilôgam sơn người thợ cần dùng là:
30 : 5 = 6 (kg)
Vậy người thợ cần 6 kilôgam sơn để đủ sơn toàn bộ mặt ngoài của chiếc thùng đó.
Câu 13
Một bể bơi có chiều dài 12 m, chiều rộng 5 m và sâu 2,75 m. Hỏi người thợ phải dùng bao nhiêu viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó? Biết rằng diện tích mạch vữa lát không đáng kể và mỗi viên gạch có chiều dài 25 cm, chiều rộng 20 cm.
Lời giải
Chu vi mặt đáy của bể bơi là:
C = 2 . (12 + 5) = 34 (m)
Diện tích xung quanh của bể bơi là:
Sxq = C . h = 34 . 2,75 = 93,5 (m2)
Diện tích mặt đáy của bể bơi là:
Sđáy = 12 . 5 = 60 (m2)
Tổng diện tích xung quanh và một mặt đáy của bể bơi là:
S = 93,5 + 60 = 153,5 (m2)
Diện tích một viên gạch men là:
20 . 25 = 500 (cm2)
Đổi: 500 cm2 = 0,05 m2.
Số viên gạch men cần dùng là:
153,5 : 0,05 = 3 070 (viên)
Vậy người thợ phải dùng 3 070 viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó.
Câu 14
Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 96 dm2. Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 3,2 m2 tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 96 dm2. Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 3,2 m2 tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Lời giải
Đổi: 3,2 m2 = 320 dm2.
Một hình lập phương gồm 6 mặt có diện tích bằng nhau.
Diện tích một mặt của hộp thiết bị là:
96 : 6 = 16 (dm2)
Gọi a (dm) là cạnh của hộp thiết bị đó nên suy ra diện tích một mặt của hộp thiết bị là a2 (dm2)
Ta có: a2 = 16 nên suy ra a = 4 (dm)
Từ đó suy ra cạnh của hộp thiết bị là 4 dm.
Thể tích một hộp đựng thiết bị là:
V1 = 43 = 64 (dm3)
Diện tích một mặt của thùng đựng hàng không có nắp là:
320 : 5 = 64 (dm2)
Gọi b (dm) là cạnh của hộp đựng thiết bị đó nên suy ra diện tích một mặt của hộp đựng thiết bị là b2 (dm2)
Ta có: b2 = 64 nên suy ra b = 8 (dm)
Từ đó suy ra cạnh của thùng đựng hàng là 8 dm.
Thể tích thùng đựng hàng là:
V2 = 83 = 512 (dm3)
Số hộp thiết bị đựng được trong một thùng là:
V2 : V1 = 512 : 64 = 8 (hộp).
Vậy mỗi thùng đựng được 8 hộp thiết bị.
Câu 15
Một nhà kính trồng hoa có hình dạng và kích thước như Hình 10.14. Nhà kính có hình dạng gồm một hình lăng trụ đứng tam giác và một hình hộp chữ nhật. Tính thể tích của nhà kính.
Một nhà kính trồng hoa có hình dạng và kích thước như Hình 10.14. Nhà kính có hình dạng gồm một hình lăng trụ đứng tam giác và một hình hộp chữ nhật. Tính thể tích của nhà kính.
Lời giải
Diện tích mặt đáy của lăng trụ đứng tam giác là:
Thể tích của lăng trụ đứng tam giác là:
V1 = S1 . h = 4,8 . 6 = 28,8 (m3)
Thể tích của hình hộp chữ nhật là:
V2 = 8 . 3,8 . 6 = 182,4 (m3)
Thể tích của nhà kính là:
V = V2 + V1 = 182,4 + 28,8 = 211,2 (m3).
Vậy thể tích của nhà kính là 211,2 m3.
4.6
253 Đánh giá
50%
40%
0%
0%
0%