Câu hỏi:
13/07/2024 347
Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD.
Chứng minh BK + CN < \(\frac{1}{2}\)(AB + BC + CA).
Chứng minh BK + CN < \(\frac{1}{2}\)(AB + BC + CA).
Quảng cáo
Trả lời:
Giải bởi Vietjack
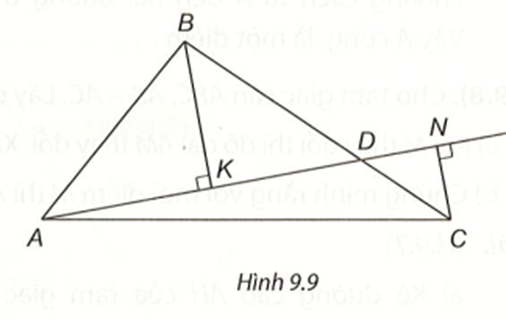
Trong tam giác vuông ABK có AB là cạnh huyền nên BK < AB. (5)
Trong tam giác vuông CAN có AC là là cạnh huyền nên CN < AC. (6)
Từ (4), (5) và (6) suy ra (BK + CN) + BK + CN < BC + AB + AC,
hay 2(BK + CN) < AB + BC + CA,
do đó BK + CN < \(\frac{1}{2}\)(AB + BC + CA).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
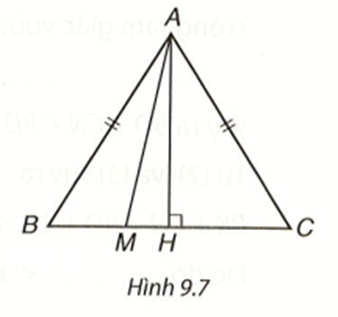
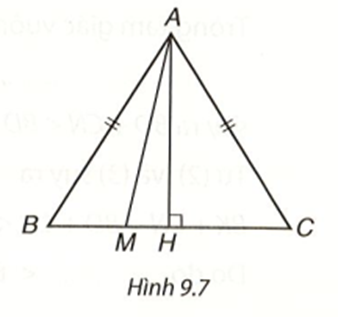
M là một điểm nằm giữa B và C. Ta cần chứng minh AM < AB. Muốn vậy, ta xét các trường hợp sau:
Trường hợp 1: Nếu \(\widehat {AMB} = 90^\circ \), thì AM là đường vuông góc, còn AB là đường xiên kẻ từ A xuống BC theo định lí về đường vuông góc và đường xiên, ta có AM < AB.
Trường hợp 2: Nếu \[\widehat {AMB}\] là góc tù thì trong tam giác AMB, góc AMB lớn nhất nên AM < AB.
Trường hợp 3: Nếu \[\widehat {AMB}\] là góc nhọn thì góc AMC kề bù với nó nên \(\widehat {AMC}\) là góc tù.
Trong tam giác AMC, góc AMC lớn nhất. Do đó AM < AC = AB.
Lời giải
Kẻ đường cao AH của tam giác ABC, ta có AH là đường vuông góc hạ từ điểm A xuống BC. Gọi M là điểm tùy ý nằm giữa B và C. Nếu M khác H thì AM là đường xiên kẻ từ A đến BC. Do đó theo định lí, AH < AM. Vậy AM nhỏ nhất bằng AH khi M trùng H.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận