Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài 10: Tứ giác có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
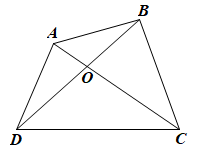
Xét tứ giác ABCD. Chu vi tứ giác ABCD là PABCD = AB + BC + CD + DA.
a) Trong ∆ABC có AC < AB + BC (bất đẳng thức trong tam giác)
Trong ∆ACD có AC < CD + DA (bất đẳng thức trong tam giác)
Do đó AC + AC < AB + BC + CD + DA hay 2AC < PABCD (1)
Tương tự, trong ∆ABD có BD < AD + AB
Trong ∆BCD có: BD < CD + BC
Do đó BD + BD < AD + AB + CD + BC hay 2BD < PABCD. (2)
Từ (1) và (2) suy ra 2(AC + BD) < 2PABCD, do đó AC + BD < PABCD.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
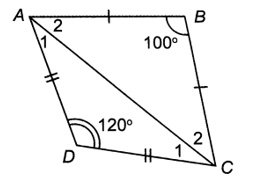
Do AB = BC nên ∆BAC cân tại B, suy ra
Xét ∆BAC có: (định lí tổng ba góc của một tam giác)
Do đó
Do CD = DA, ∆DAC cân tại D, suy ra
Xét ∆ADC có:
Do đó
Ta có:
Vậy tứ giác ABCD có
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
– Trước hết cho hai điểm phân biệt P, Q thì với mọi điểm M ta có MP + MQ ≥ PQ và MP + MQ = PQ chỉ khi M thuộc đoạn thẳng PQ.
Thật vậy,
• nếu M không thuộc đường thẳng PQ thì MP + MQ > PQ (bất đẳng thức tam giác) (hình vẽ)
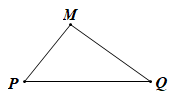
• nếu M thuộc đoạn thẳng PQ thì MP + MQ = PQ (hình vẽ)
• nếu M thuộc đường thẳng PQ nhưng không thuộc đoạn thẳng PQ thì hoặc P nằm giữa M và Q hoặc Q nằm giữa P và M, dễ thấy trong cả hai trường hợp đó, MP + MQ > PQ (hình vẽ).
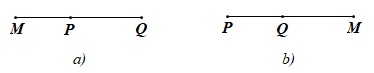
– Xét điểm M tuỳ ý trong tứ giác ABCD (hình vẽ).
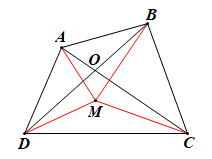
Ta có:
MA + MC ≥ AC và MA + MC = AC khi điểm M nằm trên đoạn thẳng AC.
MB + MD ≥ BD và MB + MD = BD khi điểm M nằm trên đoạn thẳng BD.
Do đó MA + MB + MC + MD ≥ AC + BD và MA + MB + MC + MD = AC + BD chỉ khi M vừa thuộc đoạn thẳng AC vừa thuộc đoạn thẳng BD tức là M phải trùng với giao điểm O của AC và BD.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập