Câu hỏi:

27/07/2023 990

a) Góc kề bù với góc tại một đỉnh của tứ giác gọi là một góc ngoài tại đỉnh đó của tứ giác. (Có hai góc ngoài tại một đỉnh của tứ giác, chúng đối đỉnh nên thường gọi tắt là góc ngoài tại đỉnh đó của tứ giác). Hãy tính tổng bốn góc ngoài tại bốn đỉnh của một tứ giác.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 KNTT Bài 10: Tứ giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

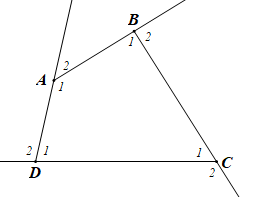
Do góc ngoài và góc tại đỉnh đó là 2 góc kề bù nên tổng bằng 180°.

Xét tứ giác ABCD (hình vẽ) có:

${\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1} = 360 °;$

Góc ngoài tại đỉnh A là ${\hat{A}}_{2} = 180 ° - {\hat{A}}_{1};$

Góc ngoài tại đỉnh B là ${\hat{B}}_{2} = 180 ° - {\hat{B}}_{1};$

Góc ngoài tại đỉnh C là ${\hat{C}}_{2} = 180 ° - {\hat{C}}_{1};$

Góc ngoài tại đỉnh D là ${\hat{D}}_{2} = 180 ° - {\hat{D}}_{1} .$

Tổng 4 góc ngoài của tứ giác ABCD là:

{\hat{A}}_{2} + {\hat{B}}_{2} + {\hat{C}}_{2} + {\hat{D}}_{2}

= (180 ° - {\hat{A}}_{1}) + (180 ° - {\hat{B}}_{1}) + (180 ° - {\hat{C}}_{1}) + (180 ° - {\hat{D}}_{1})

= 4 \cdot 180 ° - ({\hat{A}}_{1} + {\hat{B}}_{1} + {\hat{C}}_{1} + {\hat{D}}_{1})

= 2 \cdot 360 ° - 360 ° = 360 ° .

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chứng minh tổng độ dài hai đường chéo của tứ giác:

a) Bé hơn chu vi của tứ giác;

Xem đáp án

Lời giải

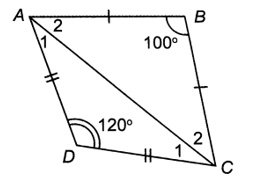
Media VietJack

Xét tứ giác ABCD. Chu vi tứ giác ABCD là P_ABCD = AB + BC + CD + DA.

a) Trong ∆ABC có AC < AB + BC (bất đẳng thức trong tam giác)

Trong ∆ACD có AC < CD + DA (bất đẳng thức trong tam giác)

Do đó AC + AC < AB + BC + CD + DA hay 2AC < P_ABCD (1)

Tương tự, trong ∆ABD có BD < AD + AB

Trong ∆BCD có: BD < CD + BC

Do đó BD + BD < AD + AB + CD + BC hay 2BD < P_ABCD. (2)

Từ (1) và (2) suy ra 2(AC + BD) < 2P_ABCD, do đó AC + BD < P_ABCD.

Câu 2

Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.

Xem đáp án

Lời giải

– Trước hết cho hai điểm phân biệt P, Q thì với mọi điểm M ta có MP + MQ ≥ PQ và MP + MQ = PQ chỉ khi M thuộc đoạn thẳng PQ.

Thật vậy,

• nếu M không thuộc đường thẳng PQ thì MP + MQ > PQ (bất đẳng thức tam giác) (hình vẽ)

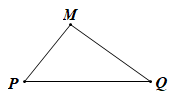
• nếu M thuộc đoạn thẳng PQ thì MP + MQ = PQ (hình vẽ)

• nếu M thuộc đường thẳng PQ nhưng không thuộc đoạn thẳng PQ thì hoặc P nằm giữa M và Q hoặc Q nằm giữa P và M, dễ thấy trong cả hai trường hợp đó, MP + MQ > PQ (hình vẽ).

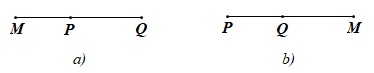
– Xét điểm M tuỳ ý trong tứ giác ABCD (hình vẽ).

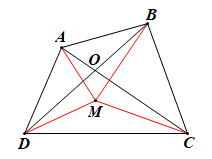
Ta có:

MA + MC ≥ AC và MA + MC = AC khi điểm M nằm trên đoạn thẳng AC.

MB + MD ≥ BD và MB + MD = BD khi điểm M nằm trên đoạn thẳng BD.

Do đó MA + MB + MC + MD ≥ AC + BD và MA + MB + MC + MD = AC + BD chỉ khi M vừa thuộc đoạn thẳng AC vừa thuộc đoạn thẳng BD tức là M phải trùng với giao điểm O của AC và BD.

Câu 3

Cho tứ giác ABCD với AB = BC, CD = DA, $\hat{B} = 100 °$ , $\hat{D} = 120 °$ . Tính $\hat{A}$ và $\hat{C} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chứng minh rằng trong một tứ giác, độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

b) Định nghĩa góc ngoài tại một đỉnh của tam giác một cách tương tự. Hỏi tổng các góc ngoài của một tam giác bằng bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Chứng minh rằng cả bốn góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Chứng minh tổng độ dài hai đường chéo của tứ giác: a) Bé hơn chu vi của tứ giác;

Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.

Cho tứ giác ABCD với AB = BC, CD = DA, B^=100°, D^=120°. Tính A^ và C^.

Chứng minh rằng trong một tứ giác, độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại.

b) Định nghĩa góc ngoài tại một đỉnh của tam giác một cách tương tự. Hỏi tổng các góc ngoài của một tam giác bằng bao nhiêu?

Chứng minh rằng cả bốn góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Chứng minh tổng độ dài hai đường chéo của tứ giác:

a) Bé hơn chu vi của tứ giác;

Cho tứ giác ABCD với AB = BC, CD = DA, $\hat{B} = 100 °$ , $\hat{D} = 120 °$ . Tính $\hat{A}$ và $\hat{C} .$