Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.
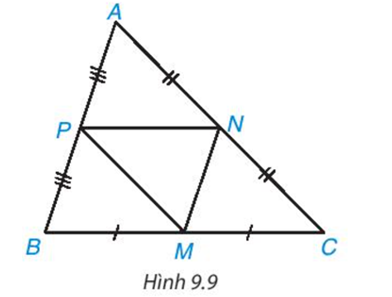
Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.

Quảng cáo
Trả lời:
- Do N, P lần lượt là trung điểm của CA, AB.
Suy ra PN là đường trung bình của tam giác ABC nên NP // BC (P ∈ AB, N ∈ AC).
Suy ra ΔABC ∽ ΔAPN.
- Do M, P lần lượt là trung điểm của BC, AB.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC (P ∈ AB, M ∈ BC)
Suy ra ΔABC ∽ ΔPBM.
- Do M, N lần lượt là trung điểm của BC, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // AB (N ∈ AC, M ∈ BC).
Suy ra ΔABC ∽ ΔNMC.
- Ta có (do ΔABC ∽ ΔPBM); (do PN // BC); (do cùng bằng góc C); .
Do đó, ΔAPN ∽ ΔPBM.
- Tương tự ta cũng có ΔNMC ∽ ΔPBM.
- - Ta có ΔAPN = ΔMNP (g – c – g) vì ; (NP // BC và các cặp góc ở vị trí so le trong) và PN cạnh chung. Do đó ΔAPN ∽ ΔMNP.
Vậy ta có 5 tam giác APN, PBM, NMC, MNP, ABC đôi một đồng dạng với nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
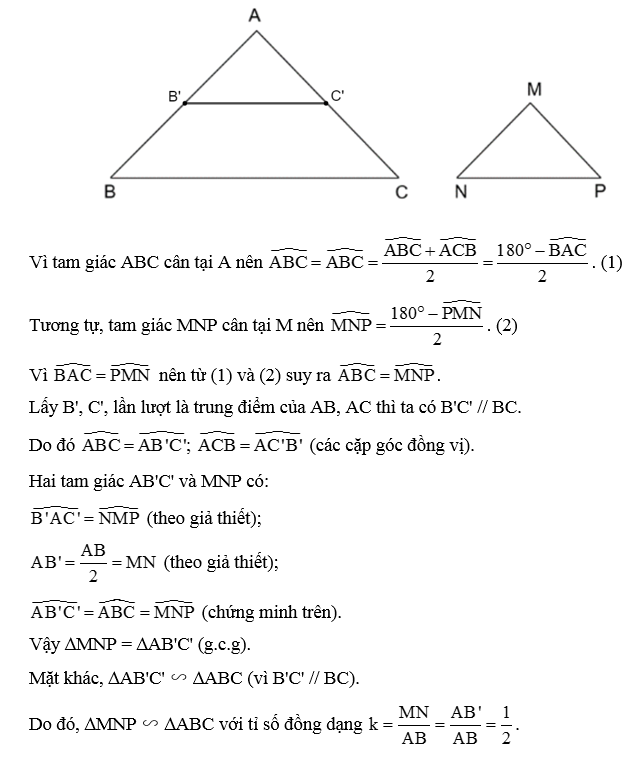
+ Khẳng định a là khẳng định đúng vì các tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên tỉ số giữa các cạnh tương ứng bằng nhau nên theo định nghĩa hai tam giác đồng dạng thì hai tam giác bằng nhau thì đồng dạng với nhau.
+ Khẳng định c là khẳng định đúng vì tam giác đều thì có các góc bằng 60° và các cạnh bằng nhau nên ta suy ra các góc tương ứng của hai tam giác đều bất kì bằng nhau và tỉ số các cạnh tương ứng của hai tam giác đều bất kì bằng nhau.
+ Khẳng định b sai vì hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
+ Khẳng định d sai vì hai tam giác vuông mới chỉ thỏa mãn một điều kiện để xét đồng dạng, cần thêm tỉ lệ cạnh tương ứng hoặc 1 góc tương ứng bằng nhau.
+ Khẳng định e sai vì hai tam giác đồng dạng chỉ có kích thước tỉ lệ với nhau, còn hai tam giác bằng nhau là có các góc, các cạnh tương ứng bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Tan Chu
Je
Tan Chu
Cảm ơn bạn
Xem tất cả 1 phản hồi
Tan Chu
Ok
Tan Chu
Jebsn
Xem tất cả 1 phản hồi
Tan Chu
C