Câu hỏi:

19/08/2025 76,226

Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn, từ A vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm).

1) Chứng minh tứ giác ABOC nội tiếp.

2) Vẽ đường kính CE, nối AE cắt đường tròn (O) tại điểm thứ hai là F.

Chứng minh AB² = AE.AF.

3) Cho OA cắt BC tại H, BF cắt OA tại I. Chứng minh I là trung điểm của AH.

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 10) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

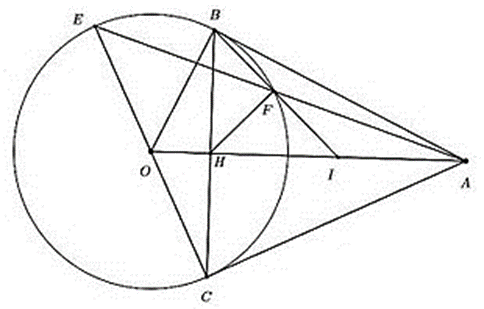
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn, từ A vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm). 1) Chứng minh tứ giác ABOC nội tiếp. (ảnh 1)

1) Xét tứ giác ABOC có:

$\hat{A B O} = \hat{A C O} = 90 °$ (AC, AB lần lượt là tiếp tuyến tại B, C của (O))

$\Rightarrow \hat{A B O} + \hat{A C O} = 180 °$

Vậy tứ giác ABOC nội tiếp (hai góc đối bù nhau).

2) Xét $Δ A B F$ và $Δ A E B$ có:

$\hat{B A F}$ là góc chung

$\hat{A B F} = \hat{A E B}$ (cùng bằng $\frac{1}{2} s đ \overset{⏜}{A F}$ của (O))

Do đó $Δ A B F ∽ Δ A E B (g . g)$

$\Rightarrow \frac{A B}{A F} = \frac{A E}{A B}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow A B^{2} = A E . A F$ .

3) Xét (O) có AB, AC lần lượt là tiếp tuyến tại B, C của (O), $O A \cap B C = H$ .

$\Rightarrow O A ⊥ B C$ tại H

Xét ABO vuông tại B, đường cao BH, ta có: $A B^{2} = A H . A O$

Do đó $A E . A F = A H . A O (= A B^{2})$

$\Rightarrow \frac{A E}{A H} = \frac{A O}{A F}$

Xét AEO và AHF, ta có:

$\hat{H A F}$ là góc chung

$\frac{A E}{A H} = \frac{A O}{A F}$

Do đó $Δ A E O ∽ Δ A H F (c . g . c)$

$\Rightarrow \hat{A E O} = \hat{A H F}$ (Hai góc tương ứng)

Mà $\hat{A H F} + \hat{F H O} = 180 °$ (hai góc kề bù)

Nên $\hat{A E O} + \hat{F H O} = 180 °$ hay $\hat{F E O} + \hat{F H O} = 180 °$

Suy ra tứ giác OHFE nội tiếp (Hai góc đối bù nhau)

$\Rightarrow \hat{H F E} + \hat{H O E} = 180 °$ (Tính chất tứ giác nội tiếp)

Kéo dài AO cắt (O) tại K (O nằm giữa A và K, ta có: $\hat{K O E} + \hat{H O E} = 180 °$ )

$\Rightarrow \hat{K O E} = \hat{H F E}$ (cùng bù $\hat{H O E}$ )

Xét (O), ta có:

$\hat{E B C} = 90 °$ (Góc nội tiếp chắn nửa đường tròn) $\Rightarrow E B ⊥ B C$

Mặt khác, ta có $O A ⊥ B C$ tại H (cmt) $\Rightarrow A K ⊥ B C$

Do đó: EB // AK (cùng vuông góc với BC) $\Rightarrow \hat{K O E} = \hat{O E B}$ (Hai góc so le trong)

$\Rightarrow \hat{K O E} = \hat{C E B}$

Suy ra $\hat{H F E} = \hat{C E B} (= \hat{K O E})$

Xét (O), ta có: $\hat{B F E} = \hat{B C E}$ (cùng bằng $\frac{1}{2} s đ \overset{⏜}{B E}$ của (O))

Trong $Δ E B C$ vuông tại B, ta có: $\hat{B E C} + \hat{B C E} = 90 °$

Ta có: $\hat{B F H} = \hat{B F E} + \hat{H F E} = \hat{B C E} + \hat{B E C} = 90 ° \Rightarrow H F ⊥ B I$ tại F

Xét tam giác BHI vuông tại H, đường cao HF, ta có:

$I H^{2} = I F . I B (1)$

Xét IAF và IBA, ta có:

$\hat{A I F}$ là góc chung

$\hat{I B A} = \hat{I A F}$ ( $\hat{I B A} = \hat{B E F}$ cùng chắn cung BF của (O), $\hat{B E F} = \hat{I A F}$ là hai góc so le trong của EF // AK)

Vậy $Δ I A F ∽ Δ I B A (g . g)$

$\Rightarrow \frac{I A}{I B} = \frac{I F}{I A} \Rightarrow I A^{2} = I F . I B (2)$

Từ (1) và (2)

=> IH = IA hay i là trung điểm ah.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cái chai có chứa một lượng nước, phần chứa nước là hình trụ có chiều cao 10cm, khi lật ngược chai lại thì phần không chứa nước cũng là một hình trụ có chiều cao 8 cm (như hình vẽ bên. Biết thể tích của chai là $450 π {cm}^{3}$ . Tính bán kính của đáy chai (giả sử độ dày của thành chai và đáy chai không đáng kể).

Xem đáp án

Lời giải

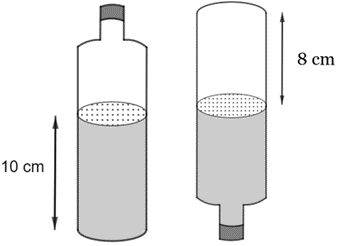
Gọi R (cm) là bán kính đáy chai (R > 0).

Thể tích nước trong chai (hình trụ có chiều cao 10 cm) là:

$V_{2} = π R^{2} . h_{2} = 8 π R^{2} ({cm}^{3})$

Thể tích không chứa nước trong chai khi lật ngược chai (hình trụ có chiều cao 8 cm) là:

$V_{2} = π R^{2} . h_{2} = 8 π R^{2} ({cm}^{3})$

Thể tích của chai $(450 π {cm}^{3})$ là tổng thể tích của nước và phần không chứa nước trong chai khi lật ngược chai lại, nên ta có: $V_{1} + V_{2} = 450 π$

$\Leftrightarrow 10 π R^{2} + 8 π R^{2} = 450 π \Leftrightarrow 18 π R^{2} = 450 π$

$\Leftrightarrow R^{2} = 25$

$\Rightarrow R = 5$ (do R > 0)

Vậy bán kính của đáy chai là 5 cm.

Câu 2

Một công ty dự định thuê một số xe lớn cùng loại để chở vừa hết 210 người đi du lịch Mũi Né. Nhưng thực tế, công ty lại thuê toàn bộ xe nhỏ hơn cùng loại. Biết rằng số xe nhỏ phải thuê nhiều hơn số xe lớn là 2 chiếc thì mới chở vừa hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người. Tính số xe nhỏ đã thuê.

Xem đáp án

Lời giải

Gọi số xe nhỏ (chiếc) công ty đã thuê là $x (x \in ℕ, x > 2)$ .

Do đó số xe lớn (chiếc) công ty dự định thuê là x - 2.

Số xe lớn và nhỏ đều chở vừa hết 210 người nên:

Số người trên xe nhỏ là: $\frac{210}{x}$ (người)

Số người trên xe lớn là: $\frac{210}{x - 2}$ (người)

Theo đề mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người, nên ta có phương trình:

$\frac{210}{x - 2} - \frac{210}{x} = 12 \Leftrightarrow 210 x - 210 (x - 2) = 12 x (x - 2) \Leftrightarrow 210 x - 210 x + 420 = 12 x^{2} - 24 x \Leftrightarrow 12 x^{2} - 24 x - 420 = 0 \Leftrightarrow 12 (x - 7) (x + 5) = 0 \Leftrightarrow [\begin{array}{l} x - 7 = 0 \\ x + 5 = 0 \end{array} \Leftrightarrow [\begin{matrix} x = 7 & (nhan) \\ x = - 5 & (loai) \end{matrix}$

Vậy công ty đã thuê 7 chiếc xe nhỏ.

Câu 3

Cho hàm số y = x² có đồ thị (P).

1) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

2) Tìm giá trị nguyên của tham số m để đường thẳng $(d) : y = 2 m x - m^{2} + 1$ cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là x₁ , x₂ thỏa mãn x₁ < 2024 < x₂.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải phương trình và hệ phương trình sau: $x^{2} + 2 x - 3 = 0$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Từ hình vuông đầu tiên, bạn Hùng vẽ hình vuông thứ hai có các đỉnh là trung điểm của các cạnh hình vuông thứ nhất, vẽ tiếp hình vuông thứ ba có các đỉnh là trung điểm của các cạnh hình vuông thứ hai và cứ tiếp tục như vậy (xem hình minh họa bên). Giả sử hình vuông thứ bảy có diện tích bằng 32 cm². Tính diện tích hình vuông thứ năm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Rút gọn các biểu thức sau: $A = (\sqrt{27} - \sqrt{12} + \sqrt{48}) \sqrt{3}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Giải phương trình và hệ phương trình sau: $x^{2} + 2 x - 3 = 0$

Rút gọn các biểu thức sau: $A = (\sqrt{27} - \sqrt{12} + \sqrt{48}) \sqrt{3}$