Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng ABC là tam giác vuông cân tại A và có cạnh bên bằng \(2\sqrt 2 \) cm.
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng ABC là tam giác vuông cân tại A và có cạnh bên bằng \(2\sqrt 2 \) cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
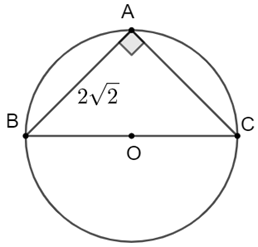
Áp dụng định lí Pythagore cho tam giác ABC vuông cân tại A, ta có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {16} = 4\) (cm).
Do đó \(R = \frac{{BC}}{2} = \frac{4}{2} = 2\) (cm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
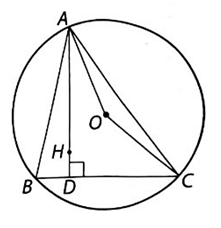
Cho AH cắt BC tại D ta được tam giác ABD vuông tại D. Khi đó
\(\widehat {BAH} = \widehat {BAD} = 90^\circ - \widehat {ABD} = 90^\circ - \widehat {ABC}.\) (1)
Mặt khác, vì ∆AOC cân tại O nên:
\(\widehat {OAC} = \widehat {OCA} = \frac{{180^\circ - \widehat {AOC}}}{2} = 90^\circ - \frac{{\widehat {AOC}}}{2} = 90^\circ - \widehat {ABC}.\) (2)
Từ (1) và (2) suy ra \(\widehat {BAH} = \widehat {OAC}.\)
Lời giải
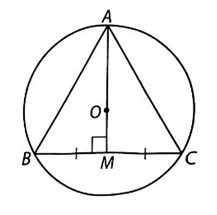
Gọi R là bán kinh đường tròn ngoại tiếp tam giác ABC.
Ta có \(R = \frac{{\sqrt 3 }}{3}BC,\) hay \(BC = \sqrt 3 R = 3\sqrt 3 \) (cm).
Gọi M là trung điểm của BC.
Ta có \(AM = \frac{{\sqrt 3 }}{2}BC = \frac{9}{2}\) cm.
Vậy \({S_{ABC}} = \frac{1}{2}AM.BC = \frac{1}{2}.\frac{9}{2}.3\sqrt 3 = \frac{{27\sqrt 3 }}{4}\) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập