Cho tam giác ABC vuông tại A, biết AB = 6 cm, AC = 8 cm.
a) Tính tan B, cạnh BC, sin B, góc B (làm tròn đến độ).
b) Kẻ đường cao AH. Tính AH, BH, \(\cos \widehat {BAH}.\)
Cho tam giác ABC vuông tại A, biết AB = 6 cm, AC = 8 cm.
a) Tính tan B, cạnh BC, sin B, góc B (làm tròn đến độ).
b) Kẻ đường cao AH. Tính AH, BH, \(\cos \widehat {BAH}.\)
Quảng cáo
Trả lời:
(H.4.9)
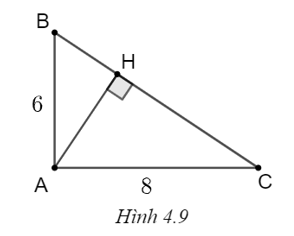
a) Trong tam giác ABC vuông có
\(\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}.\)
Theo định lí Pythagore, ta có
BC2 = AC2 + AB2 = 82 + 62 = 100.
\(BC = \sqrt {100} = 10.\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5},\) từ đó suy ra \(\widehat B \approx 53^\circ .\)
b) Trong tam giác vuông ABH có:
\(\sin B = \frac{{AH}}{{AB}},\) suy ra \(AH = AB.\sin B = 6.\frac{4}{5} = \frac{{24}}{5};\)
\(\tan B = \frac{{AH}}{{BH}},\) suy ra \(BH = \frac{{AH}}{{\tan B}} = \frac{{24}}{5}:\frac{4}{3} = \frac{{24}}{5}.\frac{3}{4} = \frac{{18}}{5}.\)
\(\cos \widehat {BAH} = \sin \widehat {ABC} = \frac{4}{3}\) (vì \(\widehat {BAH}\) và góc \(\widehat {ABC}\) là hai góc phụ nhau).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) (H.4.5a)
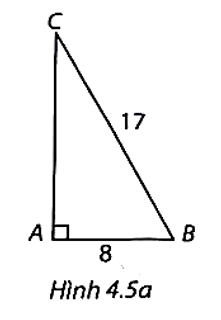
Theo định lí Pythagore, ta có
AC2 + AB2 = BC2
AC2 = BC2 – AB2
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{17}^2} - {8^2}} = \sqrt {225} = 15.\)
Từ đó:
• \(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}},\) \(\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{8}{{17}},\)
• \(\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{15}}{8},\) \(\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{8}{{15}}.\)
b) (H.4.5b)
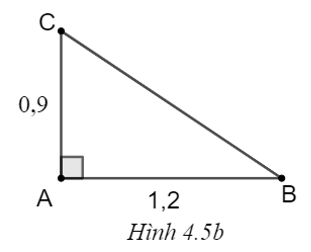
Theo Pythagore, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{1,2}^2} + {{0,9}^2}} = \sqrt {2,25} = 1,5.\)
Từ đó:
• \(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = 0,6,\)
• \(\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = 0,8,\)
\(\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = 0,75,\)
\(\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\)
Lời giải
a) Ta có sin 55° = cos(90° – 55°) = cos 35°;
cos 62° = sin(90° – 62°) = sin 28°;
tan 57° = cot(90° – 57°) = cot 33°;
cot 64° = tan(90° – 64°) = tan 26°.
b) Ta có \(\frac{{\tan 25^\circ }}{{\cot 65^\circ }} = \frac{{\tan 25^\circ }}{{\tan \left( {90^\circ - 65^\circ } \right)}} = \frac{{\tan 25^\circ }}{{\tan 25^\circ }} = 1;\)
\(\tan 34^\circ - \cot 56^\circ = \tan 34^\circ - \tan \left( {90^\circ - 56^\circ } \right) = \tan 34^\circ - \tan 34^\circ = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.