Câu hỏi:
15/09/2024 759
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.19a).
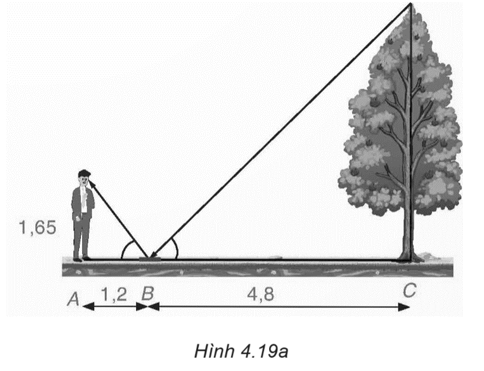
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.19a).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi A' là điểm tại mặt người đứng, C' là đỉnh ngọn cây (H.4.19b) thì theo quang học, ta có \(\widehat {ABA'} = \widehat {CBC'}.\)
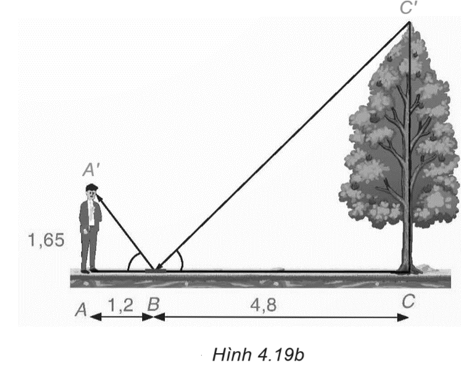
Trong tam giác ABA', ta có \(\tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{{1,65}}{{1,2}} = \frac{{11}}{8}.\)
Trong tam giác CBC', ta có \(\tan \widehat {CBC'} = \frac{{CC'}}{{BC}}.\)
Vì \(\widehat {ABA'} = \widehat {CBC'}\) nên \(\tan \widehat {ABA'} = \tan \widehat {CBC'}\) hay \(\frac{{CC'}}{{BC}} = \frac{{11}}{8},\)
suy ra \(CC' = \frac{{11.4,8}}{8} = \frac{{33}}{5} = 6,6\) (m).
Vậy chiều cao của cây là 6,6 m.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
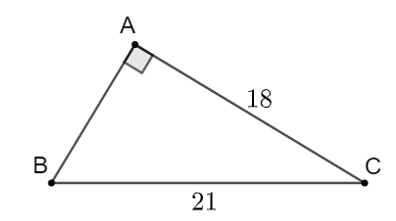
Theo định lí Pythagore, ta có \({c^2} = {21^2} - {18^2} = 117\) suy ra \(c = \sqrt {117} = 3\sqrt {13} \approx 11.\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\) nên dùng MTCT ta có \(\widehat B \approx 59^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 59^\circ \approx 31^\circ .\)
b)
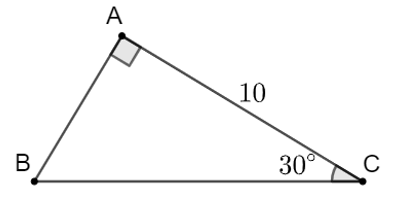
Ta có \(\widehat B = 90^\circ - \widehat C = 90^\circ - 30^\circ = 0^\circ ,\) \[\cos C = \cos 30^\circ = \frac{{AC}}{{BC}} = \frac{b}{a} = \frac{{\sqrt 3 }}{2}\] nên
\(a = \frac{{2b}}{{\sqrt 3 }} = \frac{{2.10}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{3} \approx 11,\) \(c = b.\tan C = 10.\tan 30^\circ = \frac{{10\sqrt 3 }}{3} \approx 6.\)
c)
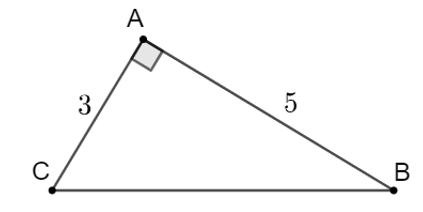
Ta có a2 = b2 + c2 = 32 + 52 = 34 nên \(a = \sqrt {34} \approx 6,\)
\(\tan B = \frac{b}{c} = \frac{3}{5},\) dùng MTCT tính được \(\widehat B \approx 31^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 31^\circ \approx 59^\circ .\)
Lời giải
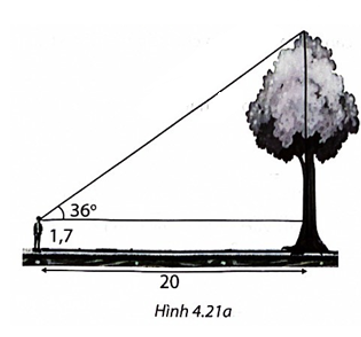
(H.4.21b)
Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
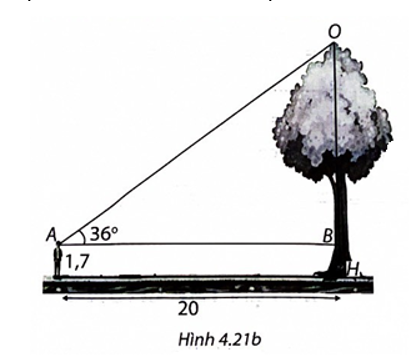
Ta có AB = 20 m và tam giác ABO vuông tại B.
Trong tam giác vuông ABO có
\(OB = AB.\tan A = 20.\tan 36^\circ \approx 14,5\) (m).
Ta có OH = OB + BH = 14,5 + 1,7 = 16,2 (m).
Vậy cây cao 16,2 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận