Câu hỏi:
15/09/2024 1,848
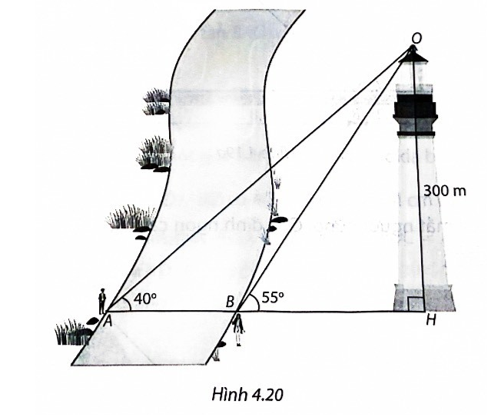
Để đo chiều rộng của một khúc sông, có hai người đã làm như sau: Hai người đứng ở hai vị trí A, B trên hai bờ sông, nhìn thấy đỉnh một tòa tháp phía xa dưới góc 40° và góc 55° (H.4.20). Biết tòa tháp cao 300 m, từ đó tính được khoảng cách AB. Em hãy cho biết, họ tính AB bằng bao nhiêu mét.
Để đo chiều rộng của một khúc sông, có hai người đã làm như sau: Hai người đứng ở hai vị trí A, B trên hai bờ sông, nhìn thấy đỉnh một tòa tháp phía xa dưới góc 40° và góc 55° (H.4.20). Biết tòa tháp cao 300 m, từ đó tính được khoảng cách AB. Em hãy cho biết, họ tính AB bằng bao nhiêu mét.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dễ thấy tam giác AHO vuông tại H.
Trong tam giác vuông AHO có
\(AH = OH.\cot A = 300.\cot 40^\circ \approx 357,5\) (m).
Trong tam giác vuông BHO có
\(BH = OH.\cot B = 300.\cot 55^\circ \approx 210,1\) (m).
Ta có AB = AH – BH = 357,5 – 210,1 = 147,4 (m).
Vậy AB = 147,4 m.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
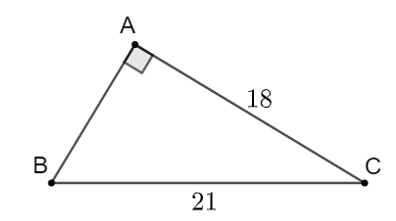
Theo định lí Pythagore, ta có \({c^2} = {21^2} - {18^2} = 117\) suy ra \(c = \sqrt {117} = 3\sqrt {13} \approx 11.\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\) nên dùng MTCT ta có \(\widehat B \approx 59^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 59^\circ \approx 31^\circ .\)
b)
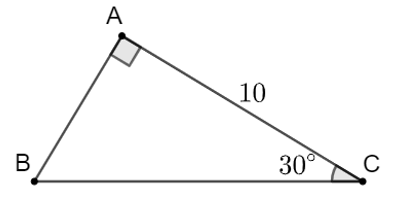
Ta có \(\widehat B = 90^\circ - \widehat C = 90^\circ - 30^\circ = 0^\circ ,\) \[\cos C = \cos 30^\circ = \frac{{AC}}{{BC}} = \frac{b}{a} = \frac{{\sqrt 3 }}{2}\] nên
\(a = \frac{{2b}}{{\sqrt 3 }} = \frac{{2.10}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{3} \approx 11,\) \(c = b.\tan C = 10.\tan 30^\circ = \frac{{10\sqrt 3 }}{3} \approx 6.\)
c)
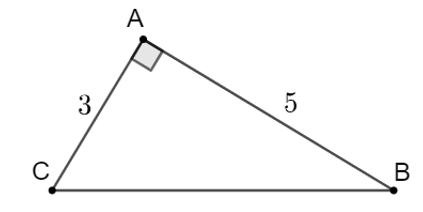
Ta có a2 = b2 + c2 = 32 + 52 = 34 nên \(a = \sqrt {34} \approx 6,\)
\(\tan B = \frac{b}{c} = \frac{3}{5},\) dùng MTCT tính được \(\widehat B \approx 31^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 31^\circ \approx 59^\circ .\)
Lời giải
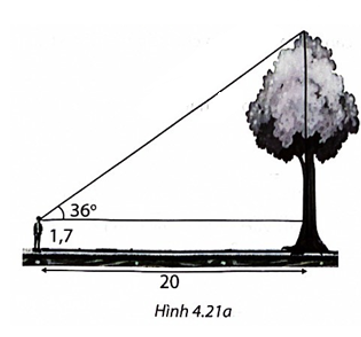
(H.4.21b)
Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
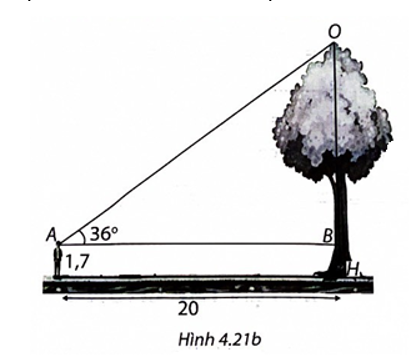
Ta có AB = 20 m và tam giác ABO vuông tại B.
Trong tam giác vuông ABO có
\(OB = AB.\tan A = 20.\tan 36^\circ \approx 14,5\) (m).
Ta có OH = OB + BH = 14,5 + 1,7 = 16,2 (m).
Vậy cây cao 16,2 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo