Quảng cáo
Trả lời:
Giải bởi Vietjack
(H.4.17)
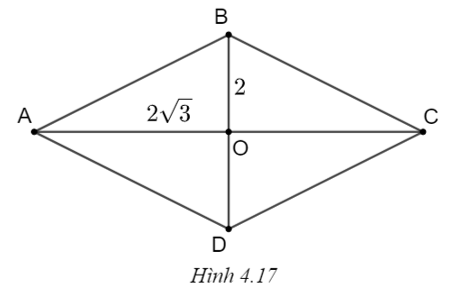
Hình thoi ABCD có \(AC = 2\sqrt 3 ,\) BD = 2.
Ta có \(AO = \frac{1}{2}AC = \frac{1}{2}.2\sqrt 3 = \sqrt 3 ,\) \(BO = \frac{1}{2}BD = \frac{1}{2}.2 = 1.\)
Dễ thấy tam giác ABO vuông tại O.
Trong tam giác vuông ABO có \(\tan \widehat {BAO} = \frac{{BO}}{{AO}} = \frac{2}{{2\sqrt 3 }} = \frac{1}{{\sqrt 3 }},\) suy ra \(\widehat {BAO} = 30^\circ ,\) do đó \(\widehat {BAD} = 2.\widehat {BAO} = 2.30^\circ = 60^\circ .\)
Do ABCD là hình thoi nên \(\widehat {ABC} = 180^\circ - \widehat {BAD} = 180^\circ - 60^\circ = 120^\circ .\)
Vậy hình thoi ABCD có một góc bằng 60° và góc kia bằng 120°.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
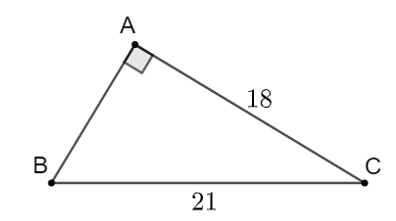
Theo định lí Pythagore, ta có \({c^2} = {21^2} - {18^2} = 117\) suy ra \(c = \sqrt {117} = 3\sqrt {13} \approx 11.\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{{18}}{{21}} = \frac{6}{7}\) nên dùng MTCT ta có \(\widehat B \approx 59^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 59^\circ \approx 31^\circ .\)
b)
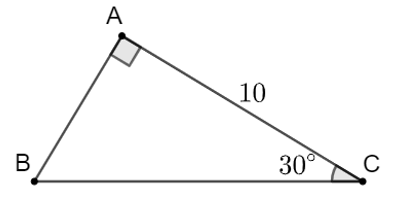
Ta có \(\widehat B = 90^\circ - \widehat C = 90^\circ - 30^\circ = 0^\circ ,\) \[\cos C = \cos 30^\circ = \frac{{AC}}{{BC}} = \frac{b}{a} = \frac{{\sqrt 3 }}{2}\] nên
\(a = \frac{{2b}}{{\sqrt 3 }} = \frac{{2.10}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{3} \approx 11,\) \(c = b.\tan C = 10.\tan 30^\circ = \frac{{10\sqrt 3 }}{3} \approx 6.\)
c)
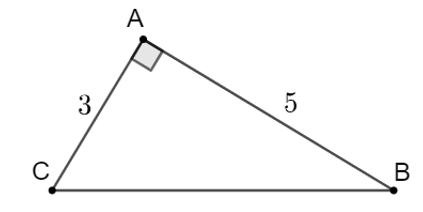
Ta có a2 = b2 + c2 = 32 + 52 = 34 nên \(a = \sqrt {34} \approx 6,\)
\(\tan B = \frac{b}{c} = \frac{3}{5},\) dùng MTCT tính được \(\widehat B \approx 31^\circ .\)
Do đó \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 31^\circ \approx 59^\circ .\)
Lời giải
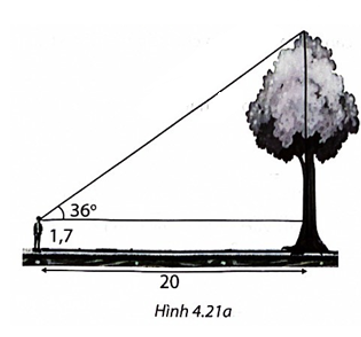
(H.4.21b)
Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
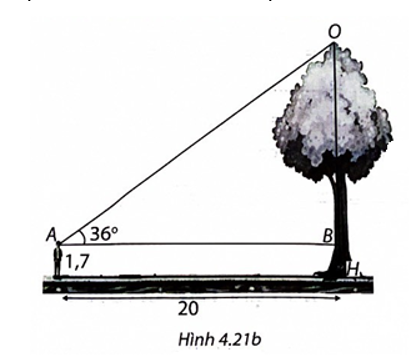
Ta có AB = 20 m và tam giác ABO vuông tại B.
Trong tam giác vuông ABO có
\(OB = AB.\tan A = 20.\tan 36^\circ \approx 14,5\) (m).
Ta có OH = OB + BH = 14,5 + 1,7 = 16,2 (m).
Vậy cây cao 16,2 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo