Câu hỏi:
15/09/2024 3,004
Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d; C và D lần lượt là điểm đối xứng với A và B qua O.
a) Ba điểm B, C và D có thuộc (O) không? Vì sao?
b) Chứng minh tứ giác ABCD là hình chữ nhật.
c) Chứng minh rằng C và D đối xứng với nhau qua d.
Quảng cáo
Trả lời:
Giải bởi Vietjack
(H.5.3)
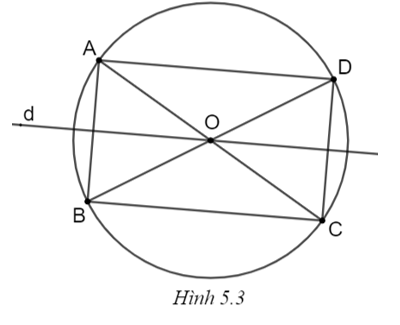
a) Vì d là một đường kính của đường tròn và B đối xứng với A qua d nên từ A ∈ (O) suy ra AB ⊥ d.
Lại có O là tâm của đường tròn và C, D lần lượt là điểm đối xứng với A, B qua O nên từ A, B ∈ (O) suy ra C và D cũng thuộc đường tròn (O).
Vậy ba điểm B, C và D thuộc đường tròn (O).
b) Vì C đối xứng với A qua O nên O là trung điểm của AC.
Vì D đối xứng với B qua O nên O là trung điểm của BD.
Tứ giác ABCD có hai đường chéo AC và BD và O là trung điểm của AC và BD nên ABCD là hình bình hành.
Lại có, AC = BD (cùng bằng đường kính của (O)).
Do đó, hình bình hành ABCD là hình chữ nhật.
c) Vì B là điểm đối xứng với A qua d nên d là đường trung trực của AB.
Hình chữ nhật ABCD có AB // CD nên d cũng là đường trung trực của CD.
Do đó C và D đối xứng với nhau qua d.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(H.5.5)
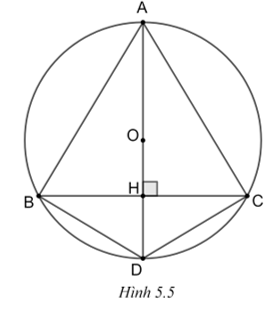
Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung trực của đoạn BC, suy ra H là trung điểm của BC.
Tam giác ACH vuông tại H nên theo định lí Pythagore, ta được
\(A{H^2} = A{C^2} - C{H^2} = A{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} = {20^2} - {\left( {\frac{{24}}{2}} \right)^2} = 256.\)
Suy ra \(AH = \sqrt {256} = 16\) (cm).
Tam giác ACD có AD là đường kính nên tam giác ACD là tam giác vuông tại C.
Trong tam giác ACD vuông tại C, ta có:
\(A{C^2} = AH.AD,\) suy ra \(AD = \frac{{A{C^2}}}{{AH}} = \frac{{{{20}^2}}}{{16}} = 25\) (cm).
Vậy bán kính của đường tròn (O) là \(R = \frac{{AD}}{2} = \frac{{25}}{2} = 12,5\) (cm).
Lời giải
(H.5.4)
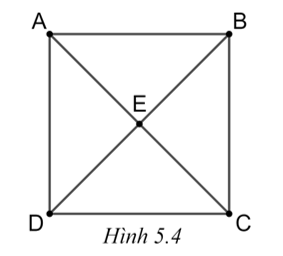
a) Do ABCD là hình vuông nên AC = BD (hai đường chéo bằng nhau), AE = BE = CE = DE (nửa đường chéo).
Do đó A, B, C, D nằm trên đường tròn tâm E.
Hai đường chéo đi qua E nên AC, BD là hai trục đối xứng của đường tròn (E).
b) Do ABC là tam giác vuông tại B, có AB = BC = 3 cm nên theo định lí Pythagore, ta được \(A{C^2} = A{B^2} + B{C^2} = {3^2} + {3^2} = 18.\)
Suy ra \(AC = \sqrt {18} = 3\sqrt 2 \) (cm).
Vậy bán kính của đường tròn (E) là \(R = \frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận