Chọn phương án đúng.
Cho hai đường tròn (O; 4 cm) và (O'; R cm) tiếp xúc ngoài nhau biết OO' = 10 cm. Khi đó:
A. R = 4 cm.
B. R = 14 cm.
C. R = 10 cm.
D. R = 6 cm.
Chọn phương án đúng.
Cho hai đường tròn (O; 4 cm) và (O'; R cm) tiếp xúc ngoài nhau biết OO' = 10 cm. Khi đó:
A. R = 4 cm.
B. R = 14 cm.
C. R = 10 cm.
D. R = 6 cm.
Quảng cáo
Trả lời:
Đáp án đúng là: D
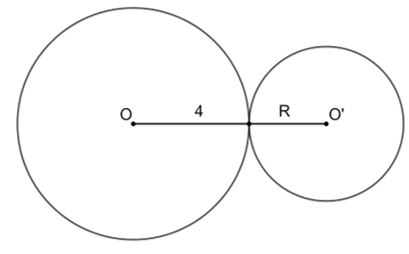
Hai đường tròn (O; 4 cm) và (O'; R cm) tiếp xúc ngoài nhau nên OO' = 4 + R = 10.
Hay R = 10 – 4 = 6 (cm).
Vậy R = 6 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(H.5.37)
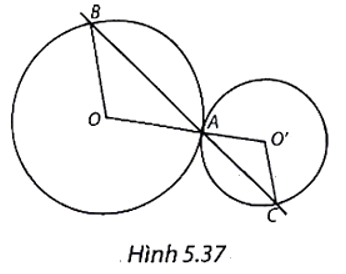
Do (O) và (O') tiếp xúc ngoài với nhau tại A nên A nằm giữa O và O'.
Do đó \(\widehat {OAB} = \widehat {O'AC}\) (hai góc đối đỉnh).
Lại có, ∆OAB cân tại O (do OA = OB).
Suy ra \(\widehat {OBA} = \widehat {OAB},\) ∆O'AC cân tại O' (do O'A = O'C) suy ra \(\widehat {O'CA} = \widehat {O'AC}.\)
Từ đó suy ra \(\widehat {OBA} = \widehat {O'CA},\) mà hai góc này ở vị trí so le trong nên OB // O'C.
Lời giải
(H.5.38)
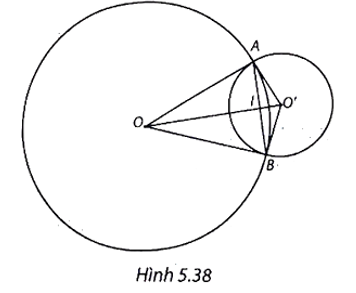
a) Vì 12 – 5 = 7 < 13 < 12 + 5 = 17 nên R – r < OO' < R + r.
Vậy hai đường tròn (O) và (O') cắt nhau tại hai điểm A, B.
Ta có: OA = OB = R và O'A = O'B = r nên OO' là đường trung trực của AB.
b) Ta có: \(O{O'^2} = {13^2} = O{A^2} + O'{A^2} = {12^2} + {5^2}\) nên tam giác AOO' vuông tại A (theo định lí Pythagore đảo), suy ra OA ⊥ O'A tại A.
Do đó OA là tiếp tuyến của (O'; r).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.