Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số

a) y = x² + 2x + 1, y = 1 – 2x và hai đường thẳng x = −1 và x = 2.

b) y = x – 4x³, y = 2x và hai đường thẳng x = 1, x = 4.

Mặt cắt ngang của lòng máng dẫn nước là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 15 (phần được tô màu xám). Tính diện tích của mặt cắt ngang đó.

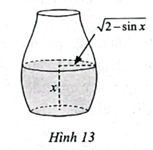
Một bình chứa nước dạng như Hình 13 có chiều cao là \[\frac{{3\pi }}{2}\] dm. Nếu lượng nước trong bình có chiều cao là x (dm) thì mặt nước là hình tròn có bán kính \[\sqrt {2 - {\mathop{\rm s}\nolimits} {\rm{inx}}} \] (dm) với 0 ≤ x ≤ \[\frac{{3\pi }}{2}\]. Tính dung tích của hình (kết quả làm tròn đến hàng phần trăm của đềximét khối).

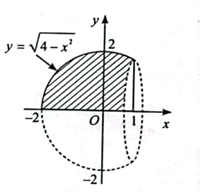
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối).

Gợi ý: có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \[y = \sqrt {4 - {x^2}} \] với −2 ≤ x ≤ 1, trục hoành và đường thẳng x = 1 quanh trục hoành.

Tính diện tích hình phẳng giới hạn bởi

a) Đồ thị của hàm số y = 3x(2 – x), trục hoành với hai đường thẳng x = −1, x = 1.

b) Đồ thị của hàm số \[y = \frac{{4 - x}}{x}\], trục hoành và hai đường thẳng x = 1, x = 2.

c) Đồ thị của hàm số y = x3 – x2 , trục hoành và hai đường thẳng x = 0, x = 2.

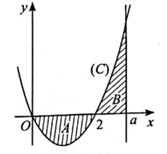
Kí hiệu S(a) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = \[\frac{3}{{{x^2}}}\], trục hoành và hai đường thẳng x = 1, x = a với a > 1 (Hình 12). Tính giới hạn \[\mathop {\lim }\limits_{a \to  + \infty } S\left( a \right)\].

Cho hàm số y = x² – 2x có đồ thị (C). Kí hiệu A là hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x = 0, x = 2; B là hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x = 2, x = a (a > 2). Tìm giá trị của a để A và B có diện tích bằng nhau.