Giải SBT Toán 12 Chân trời sáng tạo Bài 3. Ứng dụng hình học của tích phân có đáp án

a) Diện tích hình phẳng cần tìm là: \[S = \int\limits_{ - 1}^1 {\left| {3x\left( {2 - x} \right)} \right|dx}  = \int\limits_{ - 1}^1 {\left| {6x - 3{x^2}} \right|dx} \].

Ta có: 3x(2 – x) = 0 khi x = 2 hoặc x = 0.

Phương trình chỉ có nghiệm x = 0 thuộc đoạn [−1; 1].

Do đó, \[S = \int\limits_{ - 1}^1 {\left| {6x - 3{x^2}} \right|dx} \]

               \[ = \left| {\int\limits_{ - 1}^0 {\left( {6x - 3{x^2}} \right)dx} } \right| + \left| {\int\limits_{ - 1}^0 {\left( {6x - 3{x^2}} \right)dx} } \right|\]

               \[ = \left| {\left. {\left( {3{x^2} - {x^3}} \right)} \right|_{ - 1}^0} \right| + \left| {\left. {\left( {3{x^2} - {x^3}} \right)} \right|_0^1} \right|\]

               = 4 + 2 = 6.

b) Ta có \[y = \frac{{4 - x}}{x}\] > 0 với mọi x ∈ [1; 2].

Do đó diện tích hình phẳng cần tìm là:

 \[S = \int\limits_1^2 {\left| {\frac{{4 - x}}{x}} \right|} dx = \int\limits_1^2 {\left( {\frac{{4 - x}}{x}} \right)} dx\]

    \[ = \int\limits_1^2 {\left( {\frac{4}{x} - 1} \right)dx = \left. {\left( {4\ln \left| x \right| - x} \right)} \right|_1^2} \]

    = 4ln2 – 1.

c) Ta có: x3 – x2 = 0 ⇔ x2(x – 1) = 0 ⇔ x = 0 hoặc x = 1.

Với x ∈ [0; 1] thì y ≤ 0; với x ∈ [1; 2] thì y ≥ 0.

Do đó, diện tích hình phẳng cần tìm là:

\[S = \int\limits_0^2 {\left| {{x^3} - {x^2}} \right|dx} \]

  \[ = \int\limits_0^1 {\left( {{x^2} - {x^3}} \right)dx}  + \int\limits_1^2 {\left( {{x^3} - {x^2}} \right)dx} \]

  \[ = \left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^4}}}{4}} \right)} \right|_0^1 + \left. {\left( { - \frac{{{x^3}}}{3} + \frac{{{x^4}}}{4}} \right)} \right|_1^2\]

  \[ = \frac{1}{{12}} + \frac{{17}}{{12}} = \frac{3}{2}.\]

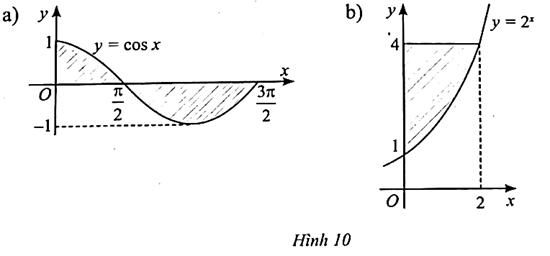
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = cosx, trục hoành và đường thẳng x = 1 và x = −1.

Diện tích hình phẳng cần tìm là:

\[S = \int\limits_0^{\frac{{3\pi }}{2}} {\left| {\cos x} \right|dx} \]

  \[ = \int\limits_0^{\frac{\pi }{2}} {\cos xdx}  + \int\limits_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( { - \cos x} \right)dx} \]

  \[ = \left. {\left( {\sin {\rm{x}}} \right)} \right|_0^{\frac{\pi }{2}} - \left. {\left( {\sin {\rm{x}}} \right)} \right|_{_{\frac{\pi }{2}}}^{^{\frac{{3\pi }}{2}}} = 3.\]

b) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2x, đường thẳng y = 4 với hai đường thẳng x = 0 và x = 2.

Diện tích hình phẳng cần tìm là:

\[S = \int\limits_0^2 {\left| {4 - {2^x}} \right|} dx = \int\limits_0^2 {\left( {4 - {2^x}} \right)dx} \]

  \[ = \left. {\left( {4x - \frac{{{2^x}}}{{\ln 2}}} \right)} \right|_0^2 = 8 - \frac{3}{{\ln 2}}.\]

a) Diện tích hình phẳng cần tìm là:

\[S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} + 2x + 1} \right) - \left( {1 - 2x} \right)} \right|} dx\]

   \[ = \int\limits_{ - 1}^2 {\left| {{x^3} + 4x} \right|} dx\].

Ta có: x2 + 4x = 0 ⇔ x = 0 hoặc x = −4. Phương trình chỉ có một nghiệm x = 0 thuộc [−1; 2].

Do đó, \[S = \int\limits_{ - 1}^2 {\left| {{x^2} + 4x} \right|dx} \]

              \[ = \int\limits_{ - 1}^0 {\left| {{x^2} + 4x} \right|dx + \int\limits_0^2 {\left| {{x^2} + 4x} \right|dx} } \]

              \[ = \left| {\int\limits_{ - 1}^0 {\left( {{x^2} + 4x} \right)dx} } \right| + \left| {\int\limits_0^2 {\left( {{x^2} + 4x} \right)dx} } \right|\]

              \[ = \left| {\left. {\left( {\frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|_{ - 1}^0} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|_0^2} \right|\]

                     \[ = \frac{5}{3} + \frac{{32}}{3} = \frac{{37}}{3}.\]

b) Diện tích hình phẳng cần tìm là:

\[S = \int\limits_1^4 {\left| {x - 4{x^3} - 2x} \right|dx = \int\limits_1^4 {\left| { - 4{x^3} - x} \right|dx} } \]

  \[ = \int\limits_1^4 {\left| { - \left( {4{x^3} + x} \right)} \right|dx}  = \int\limits_1^4 {\left| {4{x^3} + x} \right|dx} \]

Do 4x3 + x > 0 với mọi x ∈ [1; 4]. Do đó,

\[S = \int\limits_1^4 {\left| {4{x^3} + x} \right|dx} \]

   = \[\int\limits_1^4 {\left( {4{x^3} + x} \right)dx} \]

   \[ = \left. {\left( {{x^4} + \frac{{{x^2}}}{2}} \right)} \right|_1^4 = \frac{{525}}{2}.\]

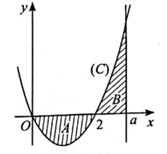
Gọi S_A, S_B lần lượt là diện tích của hình phẳng A, B. Ta có:

\[{S_A} = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx = } \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{4}{3};\]

\[{S_B} = \int\limits_2^a {\left( {{x^2} - 2x} \right)dx = \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|} _2^a\]

     \[ = \frac{{{a^3}}}{3} - {a^2} + \frac{4}{3}.\]

Theo đề bài, ta có: S_A = S_B ⇔ \[\frac{{{a^3}}}{3} - {a^2} + \frac{4}{3} = \frac{4}{3}\] hay \[\frac{{{a^3}}}{3} - {a^2} = 0\] ⇔ a = 0 hoặc a = 3.

Vì a > 2 nên a = 3 là giá trị thỏa mãn.

Diện tích hình phẳng S(a) là:

\[S\left( a \right) = \int\limits_1^a {\frac{3}{{{x^2}}}} dx\]

        \[ = 3\int\limits_1^a {\frac{1}{{{x^2}}}} dx = \left. {\frac{{ - 3}}{x}} \right|_1^a = 3\left( {1 - \frac{1}{a}} \right).\]

Ta có: \[\mathop {\lim }\limits_{a \to  + \infty } S\left( a \right) = \mathop {\lim }\limits_{a \to  + \infty } 3\left( {1 - \frac{1}{a}} \right) = 3.\]

Vậy \[\mathop {\lim }\limits_{a \to  + \infty } S\left( a \right)\] = 3.

Diện tích mặt nước hình tròn bán kính \[R = \sqrt {2 - {\mathop{\rm s}\nolimits} {\rm{inx}}} \] (dm) là:

\[S\left( x \right) = \pi {R^2} = \pi {\left( {\sqrt {2 - {\mathop{\rm s}\nolimits} {\rm{inx}}} } \right)^2} = \pi .\left( {2 - \sin {\rm{x}}} \right)\] (dm²).

Dung tích của bình là:

\[V = \int\limits_0^{\frac{{3\pi }}{2}} {S\left( x \right)dx = } \int\limits_0^{\frac{{3\pi }}{2}} {\pi \left( {2 - \sin x} \right)dx} \]

                       \[ = \left. {\pi \left( {2x + \cos x} \right)} \right|_0^{\frac{{3\pi }}{2}}\]

                                    \[ = \pi \left( {3\pi - 1} \right) \approx 26,47\] (dm³).