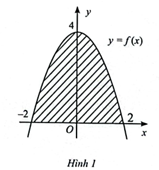
Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x; f(x)) có hệ số góc là 3x2 – 6x + 2. Tìm hàm số y = f(x), biết đồ thị của nó đi qua điểm (−1; 1).
Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x; f(x)) có hệ số góc là 3x2 – 6x + 2. Tìm hàm số y = f(x), biết đồ thị của nó đi qua điểm (−1; 1).
Quảng cáo
Trả lời:
Theo đề bài, ta có: f(−1) = 1 và f'(x) = 3x2 – 6x + 2.
Ta có \[f\left( x \right) = \int {\left( {3{x^2} - 6x + 2} \right)dx = } \] x3 – 3x2 + 2x + C.
Mà f(−1) = 1 nên (−1)3 – 3.(−1)2 + 2.(−1) + C = 1 hay C = 7.
Vậy f(x) = x3 – 3x2 + 2x + 7.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
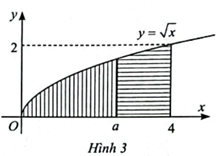
Ta có: \[S = \int\limits_0^4 {\sqrt x dx = \int\limits_0^4 {{x^{\frac{1}{2}}}dx = \left. {\frac{2}{3}\sqrt {{x^3}} } \right|_0^4} } = \frac{{16}}{3}.\]
\[{S_1} = \int\limits_0^a {\sqrt x } dx = \left. {\frac{2}{3}\sqrt {{x^3}} } \right|_0^a = \frac{2}{3}\sqrt {{a^3}} \]
Đường thẳng x = a (0 < a< 4) chia D thành hai phần có diện tích bằng nhau nên
\[{S_1} = \frac{S}{2} \Leftrightarrow \frac{2}{3}\sqrt {{a^3}} = \frac{8}{3}\]
\[ \Leftrightarrow \sqrt {{a^3}} = 4\]
\[ \Leftrightarrow {a^3} = 16 \Leftrightarrow a = 2\sqrt[3]{2}\].
Lời giải
a) Ta có:
Mà v(0) = v0 = 5 nên 3.0 + C = 5 hay C = 5.
Suy ra v(t) = 3t + 5 (m/s), do đó v(5) = 3.5 + 5 = 20 (m/s).
b) Quãng đường xe đi được trong 5 giây đầu kể từ khi tăng tốc là:
\[s = \int\limits_0^5 {v\left( t \right)dt} = \int\limits_0^5 {\left( {3t + 5} \right)dt} = \left. {\left( {\frac{3}{2}{t^2} + 5t} \right)} \right|_0^5\] = 62,5 (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.