Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288\,\,\,d{m^3}\]. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,000\] đồng/\({m^2}\). Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?

A. \[1,08\] triệu đồng.

B. \[0,91\] triệu đồng.

C. \[1,68\] triệu đồng.

D. \[0,54\] triệu đồng.

Câu hỏi trong đề: 20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

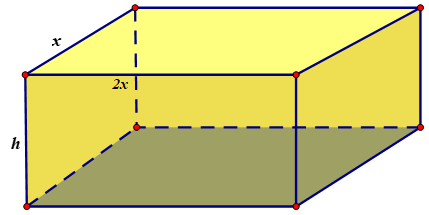
Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 d m 3 . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 000 đồng/ m 2 (ảnh 1)

Gọi \(x\) chiều rộng của đáy bể \((x > 0)\).

Khi đó chiều dài của bể là \(2x.\)

Thể tích của bể: \(V = 288\,\,\,d{m^3} = 0,288\,\,\,{m^3}\) ,

mà \(V = x.2x.h \Rightarrow h = \frac{V}{{2{x^2}}} = \frac{{0,288}}{{2{x^2}}} = \frac{{0,144}}{{{x^2}}}\) .

Phần xây dựng của bể (trừ mặt trên của bể) có diện tích:

\(S = 2.hx + 2.h.2x + x.2x = 6hx + 2{x^2} = 6.\frac{{0,144}}{{{x^2}}}.x + 2{x^2} = \frac{{0,864}}{x} + 2{x^2}\).

Xét hàm số \(S(x) = \frac{{0,864}}{x} + 2{x^2}\,\,\,,x > 0.\)

Đạo hàm: \(y' = - \frac{{0,864}}{{{x^2}}} + 4x = \frac{{4{x^3} - 0,864}}{{{x^2}}};\,\,\,y' = 0 \Leftrightarrow 4{x^3} - 0,864 = 0 \Leftrightarrow x = \frac{3}{5} = 0,6\,\,\,m.\)

Bảng biến thiên:

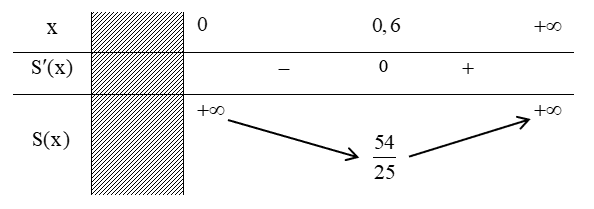
Vậy \({S_{Min}} = \frac{{54}}{{25}}\,\,\,{m^2} \Rightarrow \) Chi phí thấp nhất phải trả: \(\frac{{54}}{{25}}.500\,\,000 = 1\,\,080\,\,000\) đồng.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần. Gọi p (triệu đồng) là giá của mỗi ti vi, x là số ti vi. Khi đó hàm cầu là:

A. \(p = - \frac{1}{{200}}x + 19\).

B. \(p = \frac{1}{{200}}x + 19\).

C. \(p = - \frac{1}{{200}} + 19x\).

D. \(p = - \frac{1}{{200}}x - 19\).

Lời giải

Đáp án đúng là: A

p (triệu đồng) là giá của mỗi ti vi, x là số ti vi.

Theo giả thiết tốc độ thay đổi của x tỉ lệ với tốc độ thay đổi của p nên hàm số p = p(x) là hàm số bậc nhất. Do đó p(x) = ax + b (a ≠ 0)

Theo đề ta có: x₁ = 1000 thì p₁ = 14; x₂ = 1100 thì p₁ = 13,5.

Vì đường thẳng p = ax + b đi qua hai điểm (1000; 14) và (1100; 13,5) nên ta có hệ phương trình

\(\left\{ \begin{array}{l}1000a + b = 14\\1100a + b = 13,5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{{200}}\\b = 19\end{array} \right.\).

Vậy \(p = - \frac{1}{{200}}x + 19\).

Câu 2