Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 – 3x2 + (4 – m)x đồng biến trên khoảng (2; +∞) là A. (−∞; 1]; B. (−∞; 4]; C. (−∞; 1); D. (−∞; 4).

Đáp án đúng là: BTa có y' = 3x2 – 6x + 4 – m.Yêu cầu bài toán y' ≥ 0, ∀x ∈ (2; +∞) 3x2 – 6x + 4 – m ≥ 0, ∀x ∈ (2; +∞) m ≤ 3x2 – 6x + 4, ∀x ∈ (2; +∞) m ≤ ( mathop { min } limits_{ left( {2; + infty } right)} g left( x right) ) với g(x) = 3x2 – 6x + 4.Ta có g'(x) = 6x – 6; g'(x) = 0 6x – 6 = 0 x = 1.Dựa vào bảng biến thiên, suy ra: m ≤ 4 thỏa yêu cầu bài toán.Vậy: m ∈ (−∞; 4] thì hàm số đồng biến trên khoảng (2; +∞).

Câu hỏi:

10/01/2025 5,632

Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x³ – 3x² + (4 – m)x đồng biến trên khoảng (2; +∞) là

A. (−∞; 1];

B. (−∞; 4];

C. (−∞; 1);

D. (−∞; 4).

Xem lời giải

Câu hỏi trong đề: 12 bài tập Một số bài toán liên quan đến tính đơn điệu, cực trị có chứa tham số có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: B

Ta có y' = 3x² – 6x + 4 – m.

Yêu cầu bài toán y' ≥ 0, ∀x ∈ (2; +∞)

3x² – 6x + 4 – m ≥ 0, ∀x ∈ (2; +∞)

m ≤ 3x² – 6x + 4, ∀x ∈ (2; +∞)

m ≤ \(\mathop {\min }\limits_{\left( {2; + \infty } \right)} g\left( x \right)\) với g(x) = 3x² – 6x + 4.

Ta có g'(x) = 6x – 6; g'(x) = 0 6x – 6 = 0 x = 1.

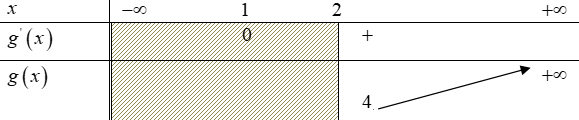
Dựa vào bảng biến thiên, suy ra: m ≤ 4 thỏa yêu cầu bài toán.

Vậy: m ∈ (−∞; 4] thì hàm số đồng biến trên khoảng (2; +∞).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tổng các giá trị nguyên của tham số m ∈ [−10; 10) để hàm số y = x³ − 3x² +3(m + 2)x + 3m – 2025 đồng biến trên trên ℝ là:

A. 27;

B. 35;

C. 44;

D. 54.

Lời giải

Đáp án đúng là: C

y = x³ − 3x² +3(m + 2)x + 3m – 2025

Hàm số đã cho xác định trên D = ℝ.

Để hàm số đồng biến trên ℝ y' = 3x² – 6x + 3(m + 2) ≥ 0, ∀x ∈ ℝ

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a > 0}\\{\Delta ' \le 0}\end{array}{\rm{ }} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3 > 0{\rm{ }}}\\{9 - 9(m + 2) \le 0}\end{array} \Leftrightarrow m \ge - 1{\rm{ }}} \right.} \right.\].

Vậy m ≥ −1 thì hàm số đồng biến trên ℝ.

Do m ∈ [−10; 10), m ∈ ℤ nên tổng các giá trị nguyên của tham số là 44.

Câu 2

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = \frac{{ - 3}}{4}{x^4} + \frac{9}{2}{x^2} - \left( {2m + 15} \right)x - m + 3\) nghịch biến trên khoảng (0; +∞)?

A. 2;

B. 3;

C. 4;

D. 5.

Lời giải

Đáp án đúng là: C

Yêu cầu bài toán y' = −3x³ + 9x – 2m – 15 ≤ 0, ∀x ∈ (0; +∞) và dấu bằng xảy ra tại hữu hạn điểm thuộc (0; +∞) 3x³ − 9x + 15 ≥ – 2m, ∀x ∈ (0; +∞).

Xét hàm số g(x) = 3x³ − 9x + 15 trên (0; +∞).

Ta có: g'(x) = 9x² – 9; g'(x) = 0 x = 1 hoặc x = −1 (loại).

Bảng biến thiên:

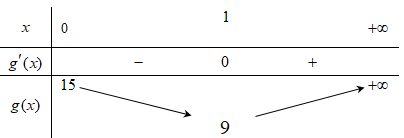
Từ bảng biến thiên ta có: \( - 2m \le 9 \Leftrightarrow m \ge - \frac{9}{2}\).

Vậy m ∈ {−4; −3; −2; −1}.

Câu 3

Biết giá trị tham số \(m \in \left[ {a;\frac{b}{c}} \right]\) (với a, b, c ∈ ℤ và \(\frac{b}{c}\) là phân số tối giản) thì hàm số y = x³ – (2m – 1)x² + (2 – m)x + 2 đồng biến trên trên ℝ. Giá trị biểu thức \(P = \frac{{{a^2} + {b^2}}}{c}.\)

A. \(P = \frac{9}{4}\);

B. \(P = \frac{{13}}{2}\);

C. P = 4;

D. \(P = \frac{{13}}{4}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + {m^2}}}{{x + 4}}\) đồng biến trên từng khoảng xác định của nó

A. 2;

B. 3;

C. 4;

D. 5.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Có bao nhiêu giá trị nguyên âm của tham số m ∈ [−2020; 2020) để hàm số y = mx³ + 3mx² – (m – 1)x – 1 có cực trị?

A. 2038;

B. 2020;

C. 2018;

D. 2021.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tìm m để hàm số \(f(x) = \frac{1}{3}{x^3} + m{x^2} + 4x + 3\) đồng biến trên ℝ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 – 3x2 + (4 – m)x đồng biến trên khoảng (2; +∞) là

Tổng các giá trị nguyên của tham số m ∈ [−10; 10) để hàm số y = x3 − 3x2 +3(m + 2)x + 3m – 2025 đồng biến trên trên ℝ là:

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = \frac{{ - 3}}{4}{x^4} + \frac{9}{2}{x^2} - \left( {2m + 15} \right)x - m + 3\) nghịch biến trên khoảng (0; +∞)?

Biết giá trị tham số \(m \in \left[ {a;\frac{b}{c}} \right]\) (với a, b, c ∈ ℤ và \(\frac{b}{c}\) là phân số tối giản) thì hàm số y = x3 – (2m – 1)x2 + (2 – m)x + 2 đồng biến trên trên ℝ. Giá trị biểu thức \(P = \frac{{{a^2} + {b^2}}}{c}.\)

Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + {m^2}}}{{x + 4}}\) đồng biến trên từng khoảng xác định của nó

Có bao nhiêu giá trị nguyên âm của tham số m ∈ [−2020; 2020) để hàm số y = mx3 + 3mx2 – (m – 1)x – 1 có cực trị?

Tìm m để hàm số \(f(x) = \frac{1}{3}{x^3} + m{x^2} + 4x + 3\) đồng biến trên ℝ.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x³ – 3x² + (4 – m)x đồng biến trên khoảng (2; +∞) là

Tổng các giá trị nguyên của tham số m ∈ [−10; 10) để hàm số y = x³ − 3x² +3(m + 2)x + 3m – 2025 đồng biến trên trên ℝ là:

Biết giá trị tham số \(m \in \left[ {a;\frac{b}{c}} \right]\) (với a, b, c ∈ ℤ và \(\frac{b}{c}\) là phân số tối giản) thì hàm số y = x³ – (2m – 1)x² + (2 – m)x + 2 đồng biến trên trên ℝ. Giá trị biểu thức \(P = \frac{{{a^2} + {b^2}}}{c}.\)

Có bao nhiêu giá trị nguyên âm của tham số m ∈ [−2020; 2020) để hàm số y = mx³ + 3mx² – (m – 1)x – 1 có cực trị?