Câu hỏi:
10/01/2025 174
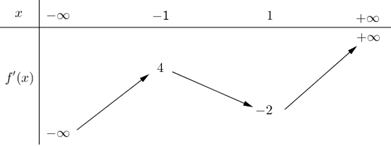
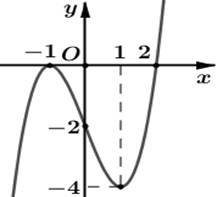
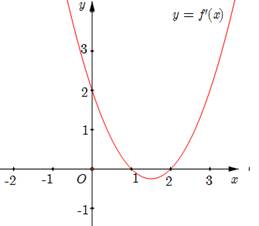
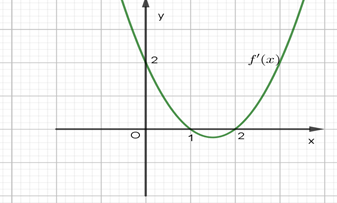
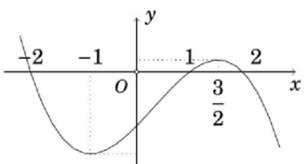
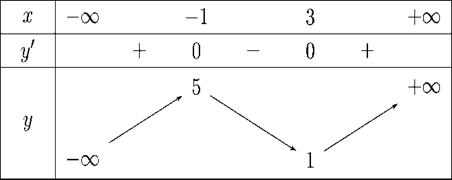
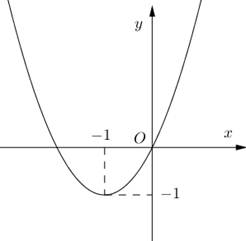
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1 có đồ thị như hình vẽ sau:
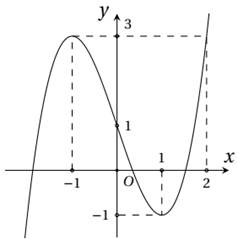
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1 có đồ thị như hình vẽ sau:
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Do hàm số y = f(x) có đúng hai điểm cực trị x = −1; x = 1 nên phương trình f'(x) = 0 có hai nghiệm bội lẻ phân biệt x = −1; x = 1.
Ta có y' = (2x – 2)f'(x2 – 2x + 1) .
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}2x - 2 = 0\\{x^2} - 2x + 1 = - 1\\{x^2} - 2x + 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\\x = 2\end{array} \right.\).
Ta có
\[y' > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2x - 2 > 0\\f'({x^2} - 2x + 1) > 0\end{array} \right.\\\left\{ \begin{array}{l}2x - 2 < 0\\f'({x^2} - 2x + 1) < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 1\\\left[ \begin{array}{l}{x^2} - 2x + 1 > 1\\{x^2} - 2x + 1 < - 1\end{array} \right.\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\ - 1 < {x^2} - 2x + 1 < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 1\\\left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\0 < x < 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 2\\0 < x < 1\end{array} \right.\].
Do đó ta có bảng biến thiên:
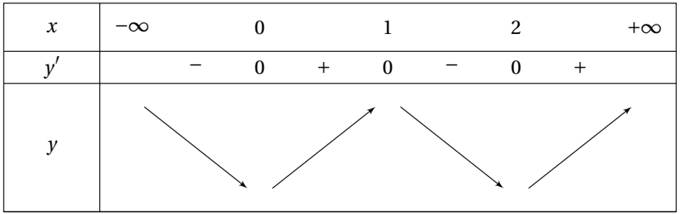
Từ bảng biến thiên ta suy ra hàm số y = f(x2 – 2x + 1) có 3 cực trị.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
Số điểm cực trị của hàm số y = f(x2 + 2x) là
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
Số điểm cực trị của hàm số y = f(x2 + 2x) là
Xem đáp án »
10/01/2025
3,419
Câu 2:
Cho hàm số y = f(x) có đồ thị y = f'(x) như hình sau. Hàm số g(x) = f(3 – 2x) + 2024 đồng biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có đồ thị y = f'(x) như hình sau. Hàm số g(x) = f(3 – 2x) + 2024 đồng biến trên khoảng nào dưới đây?
Xem đáp án »
10/01/2025
778
Câu 3:
Cho hàm số y = f'(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 – 2x) trên khoảng (0; +∞).
Cho hàm số y = f'(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 – 2x) trên khoảng (0; +∞).
Xem đáp án »
10/01/2025
378
Câu 4:
Cho hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f(2) = f(−2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ bên dưới.
Hàm số g(x) = (f(x))2 nghịch biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f(2) = f(−2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ bên dưới.
Hàm số g(x) = (f(x))2 nghịch biến trên khoảng nào dưới đây?
Xem đáp án »
10/01/2025
291
Câu 5:
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
Số điểm cực trị của hàm số y = f(x2 – 4x + 1) là:
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
Số điểm cực trị của hàm số y = f(x2 – 4x + 1) là:
Xem đáp án »
10/01/2025
217
Câu 6:
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
Xem đáp án »
10/01/2025
155
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận