Một nhóm thợ đóng giày dự định hoàn thành kế hoạch trong 26 ngày. Nhưng do cải tiến kĩ thuật nên mỗi ngày đã vượt mức 6 đôi giày, do đó chẳng những nhóm thợ đã hoàn thành kế hoạch đã định trong 24 ngày mà còn vượt mức 104 đôi giày. Tính số đôi giày nhóm thợ phải làm theo kế hoạch.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Gọi \(x\) là số đôi giày mà nhóm thợ đóng được mỗi ngày theo kế hoạch \(\left( {{\rm{x}} \in {\mathbb{N}^*}} \right)\).
Số đôi giày đóng được theo kế hoạch là \(26x\) (đôi giày).
Số đôi giày mỗi ngày đóng được thực tế là \(x + 6\) (đôi giày).
Tổng số đôi giãy đóng được thực tế \(26x + 104\) (đôi giày).
Vìnhóm thợ hoàn thành công việc trong 24 ngày nên ta có phương trình:\(\frac{{26x + 104}}{{x + 6}} = 24\)
Giải phương trình, ta được \({\rm{x}} = 20\) (thoả mãn).
Vậy số đôi giày phải đóng theo kế hoạch là \(26.20 = 520\) (đôi giày).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
Gọi \(x\) (sản phẩm/giờ) là năng suất dự định của người công nhân đó với \(x \in {\mathbb{N}^{\rm{*}}}\). Khi đó, năng suất thực tế của người đó là \(x + 3\) (sản phẩgiờ).
Theo giả thiết, ta có phương trình: \(\frac{{14}}{x} = \frac{{21}}{{x + 3}}\).
Giải phương trình:
\[\begin{array}{*{20}{r}}{\frac{{14}}{x}}&{\; = \frac{{21}}{{x + 3}}}\\{\frac{{14\left( {x + 3} \right)}}{{x\left( {x + 3} \right)}}}&{\; = \frac{{21x}}{{x\left( {x + 3} \right)}}}\\{14\left( {x + 3} \right)}&{\; = 21x}\\{14x + 42}&{\; = 21x}\\{7x}&{\; = 42}\\x&{\left. { = 6{\rm{ }}\;{\rm{ (tho}}a{\rm{ }}\;{\rm{ m }}\widetilde {\rm{a}}{\rm{ n }}\;{\rm{ }}x \in {\mathbb{N}^{\rm{*}}}} \right).}\end{array}\]
Vậy năng suất dự định của người công nhân đó là 6 sản phẩm/giờ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
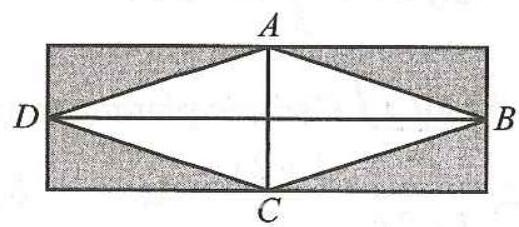
Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài của khu đất với \(x > 16\). Khi đó, chiều rộng của khu đất là \(x - 16\left( {{\rm{\;m}}} \right)\) và mảnh vườn trồng hoa có \(AC = x - 16\left( {{\rm{\;m}}} \right)\) và \(BD = x\left( {{\rm{\;m}}} \right)\).
Do đó, diện tích của khu đất là: \(\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\) và diện tích của mảnh vườn trồng hoa là: \(\frac{1}{2}\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\). Vì diện tích của phần đất còn lại là \(96{\rm{\;}}{{\rm{m}}^2}\) nên ta có phương trình: \(\left( {x - 16} \right)x - \frac{1}{2}\left( {x - 16} \right)x = 96\) hay \(\frac{1}{2}\left( {x - 16} \right)x = 96\). Tức là, \({x^2} - 16x - 192 = 0\).
Giải phương trình:
\({x^2} - 16x - 192 = 0\)
\(\left( {{x^2} - 16x + 64} \right) - 256 = 0\)
\({(x - 8)^2} - {16^2} = 0\)
\(\left( {x - 24} \right)\left( {x + 8} \right) = 0\)
\[x = 24\] hoặc \(x\)\( = - 8\)
Do \(x > 16\) nên \(x = 24\). Vậy chiều dài của khu đất là \(24{\rm{\;m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập