Hai người cùng làm chung một công việc thì xong trong 8 giờ. Hai người cùng làm được 4 giờ thì người thứ nhất bị điều đi làm công việc khác. Người thứ hai tiếp tục làm việc trong 12 giờ nữa thì xong công việc. Gọi $x$ là thời gian người thứ nhất làm một mình xong công việc (đơn vị tính là giờ, $x > 0$ ).

a) Hãy biểu thị theo $x$ :

- Khối lượng công việc mà người thứ nhất làm được trong 1 giờ;

- Khối lượng công việc mà người thứ hai làm được trong 1 giờ.

b) Hãy lập phương trình theo $x$ và giải phương trình đó. Sau đó cho biết, nếu làm một mình thì mổi người phải làm trong bao lâu mới xong công việc đó.

Xem lời giải

Câu hỏi trong đề: 22 bài tập Phương trình quy về phương trình bậc nhất một ẩn có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

a) Do x là thời gian người thứ nhất làm một mình xong công việc (đơn vị tính là giờ, x $ > 0$ ) nên khối lượng công việc mà người thứ nhất làm được trong 1 giờ là $\frac{1}{x}$ (công việc).

Hai người cùng làm chung một công việc thì xong trong 8 giờ nên khối lượng công việc mà hai người làm được trong 1 giờ là $\frac{1}{8}$ (công việc).

Khi đó, khối lượng công việc mà người thứ hai làm được trong 1 giờ là $\frac{1}{8} - \frac{1}{x}$ (công việc).

b) Hai người cùng làm trong 4 giờ được khối lượng công việc là $4 \cdot \frac{1}{8} = \frac{1}{2}$ (công việc).

Người thứ hai tiếp tục làm việc trong 12 giờ được khối lượng công việc là $12 \cdot \left( {\frac{1}{8} - \frac{1}{x}} \right) = \frac{3}{2} - \frac{{12}}{x}$ (công việc).

Theo bài, ta có phương trình: $\frac{1}{2} + \left( {\frac{3}{2} - \frac{{12}}{x}} \right) = 1$. (*)

Giải phương trình (*):$\frac{1}{2} + \left( {\frac{3}{2} - \frac{{12}}{x}} \right) = 1 \Leftrightarrow \frac{1}{2} + \frac{3}{2} - \frac{{12}}{x} = 1 \Leftrightarrow \frac{4}{2} - \frac{{12}}{x} = 1 \Leftrightarrow 2 - 1 = \frac{{12}}{x} \Leftrightarrow 1 = \frac{{12}}{x}$

Suy ra $x = 12$. Giá trị $x = 12$ thỏa mãn điều kiện $x > 0$.Khi đó, khối lượng công việc mà người thứ hai làm được trong 1 giờ là $\frac{1}{8} - \frac{1}{{12}} = \frac{3}{{24}} - \frac{2}{{24}} = \frac{1}{{24}}$ (công việc).

Vậy nếu làm một mình, để hoàn thành công việc thì người thứ nhất cần 12 giờ và người thứ hai cần 24 giờ.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một khu đất có dạng hình chữ nhật với chiều dài hơn chiều rộng $16{\rm{\;m}}$. Trên khu đất đó, người ta làm một mảnh vườn trồng hoa có dạng hình thoi $ABCD$ với đường chéo $AC$ bằng chiều rộng của khu đất và đường chéo $BD$ bằng chiều dài của khu đất (Hình 1). Tính chiều dài của khu đất, Hinh 1 biết diện tích của phần đất còn lại là $96{\rm{\;}}{{\rm{m}}^2}$.

$Một khu đất có dạng hình chữ nhật với chiều dài hơn chiều rộng $16{\rm{\;m}}$. Trên khu đất đó, người ta làm một mảnh vườn trồng hoa có dạng hình thoi $ABCD$ với đường chéo $AC$ bằng ch (ảnh 1)$

Xem đáp án

Lời giải

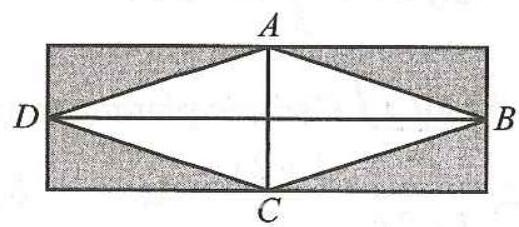
Gọi $x\left( {{\rm{\;m}}} \right)$ là chiều dài của khu đất với $x > 16$. Khi đó, chiều rộng của khu đất là $x - 16\left( {{\rm{\;m}}} \right)$ và mảnh vườn trồng hoa có $AC = x - 16\left( {{\rm{\;m}}} \right)$ và $BD = x\left( {{\rm{\;m}}} \right)$.

Do đó, diện tích của khu đất là: $\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)$ và diện tích của mảnh vườn trồng hoa là: $\frac{1}{2}\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)$. Vì diện tích của phần đất còn lại là $96{\rm{\;}}{{\rm{m}}^2}$ nên ta có phương trình: $\left( {x - 16} \right)x - \frac{1}{2}\left( {x - 16} \right)x = 96$ hay $\frac{1}{2}\left( {x - 16} \right)x = 96$. Tức là, ${x^2} - 16x - 192 = 0$.

Giải phương trình:

${x^2} - 16x - 192 = 0$

$\left( {{x^2} - 16x + 64} \right) - 256 = 0$

${(x - 8)^2} - {16^2} = 0$

$\left( {x - 24} \right)\left( {x + 8} \right) = 0$

\[x = 24\] hoặc $x$$ = - 8$

Do $x > 16$ nên $x = 24$. Vậy chiều dài của khu đất là $24{\rm{\;m}}$.

Câu 2