Một xe tải có chiều rộng là \(2,4\;{\rm{m}}\) chiều cao là \(2,5\;{\rm{m}}\) muốn đi qua một cái cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4 m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là \(2\sqrt 5 \;{\rm{m}}\) (bỏ qua độ dày của cổng).
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?
a) Trong mặt phẳng tọa độ \(Oxy\) gọi parabol \((P):y = a{x^2}\) với a \( < 0\) là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh \(a = - 1\).
b) Hỏi xe tải có đi qua cổng được không? Tại sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét vuông tại \(A\), ta có: \({\rm{OA}} = \sqrt {{\rm{O}}{{\rm{M}}^2} - {\rm{A}}{{\rm{M}}^2}} = \sqrt {{{(2\sqrt 5 )}^2} - {2^2}} = 4\;{\rm{m}}\).
\( \Rightarrow {\rm{M}}(2; - 4) \in (P):y = a{x^2} \Rightarrow - 4 = a{.2^2} \Rightarrow a = - 1\).
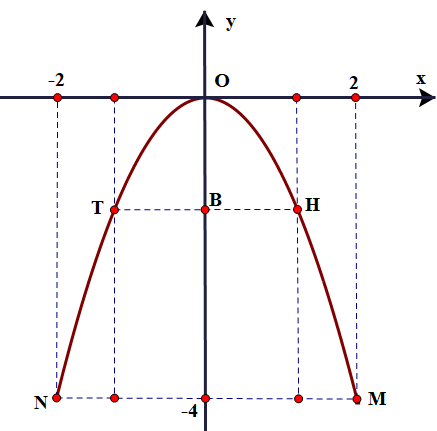
\( \Rightarrow {\rm{AB}} = 2,5\;{\rm{m}} \Rightarrow {\rm{OB}} = {\rm{OA}} - {\rm{AB}} = 4 - 2,5 = 1,5\;{\rm{m}}\)
\(({\rm{HT}}):y = - \frac{3}{2}\)
Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ: \(\left\{ {\begin{array}{*{20}{l}}{y = - {x^2}}\\{y = - \frac{3}{2}}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} = \frac{3}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array}} \right.} \right.\) hay \(\left\{ {\begin{array}{*{20}{l}}{x = - \frac{{3\sqrt 2 }}{2}}\\{y = - \frac{3}{2}}\end{array} \Rightarrow H\left( {\frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right),T\left( { - \frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right)} \right.\)
\( \Rightarrow {\rm{HT}} = 3\sqrt 2 \approx 4,24\;{\rm{m}} > 2,4\;{\rm{m}}.\)Vậy xe tải có thể đi qua cổng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
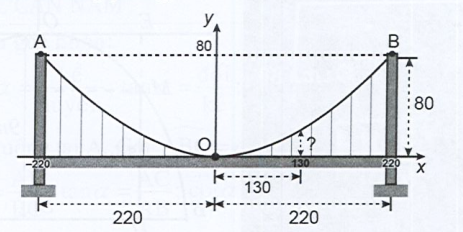
\({\rm{B}}( - 3; - 9) \in (P):y = a{x^2} \Rightarrow - 9 = a \cdot {( - 3)^2} \Rightarrow a = - 1\)
\((P):y = - {x^2}\)
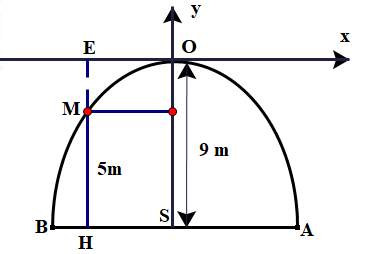
Khi banh đạt độ cao 5 m thì \({\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 9 - 5 = 4\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_M}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = - \sqrt 4 = - 2\)
Vậy sau 1 giây kể từ khi bóng được đá lên thì đạt độ cao 5 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
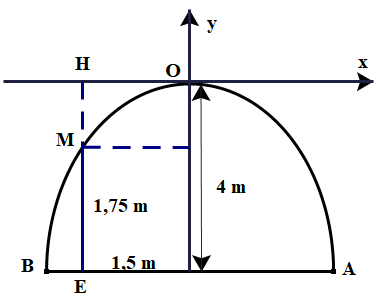
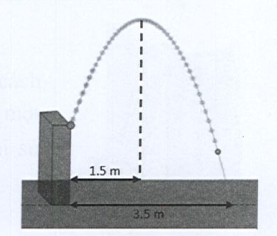
\({\rm{MH}} = {\rm{HE}} - {\rm{ME}} = 4 - 1,75 = 2,25\)
\( \Rightarrow {\rm{M}}( - 1,5; - 2,25) \in (P):y = a{x^2}\)\( \Rightarrow - 2,25 = a \cdot {( - 1,5)^2} \Rightarrow a = \frac{{ - 2,25}}{{{{( - 1,5)}^2}}} = - 1\)\((P):y = - {x^2}\)
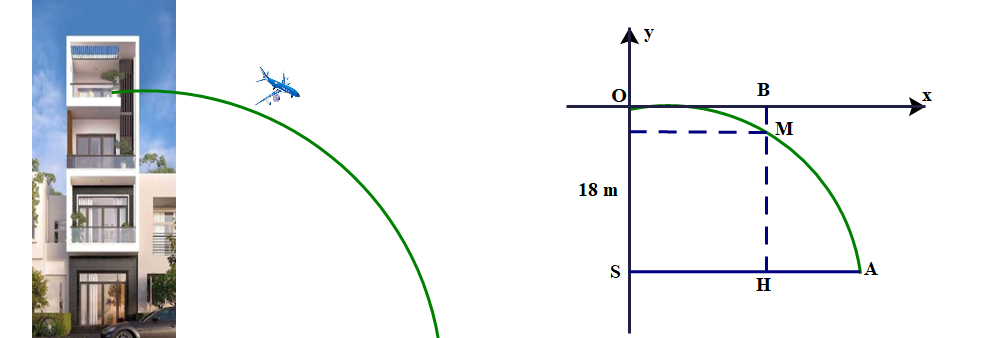
\( \Rightarrow {\rm{A}}\left( {{x_A}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = \sqrt 4 = 2\;{\rm{m}}\)
\({\rm{EA}} = {\rm{ES}} + {\rm{SA}} = 2 + 1,5 = 3,5\)
Vậy nước rơi xuống đất cách chân tháp một khoảng là \(3,5\;{\rm{m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập