Đạp xe là một hình thức tập thể dục đơn giản, rất tốt cho sức khỏe và thân thiện với môi trường. Sáng sớm, Mai dự định đạp xe từ nhà ra Hồ Gươm rồi lại đạp xe về để tập thể dục. Khi ra đến Hồ Gươm, bạn dừng lại nghỉ 3 phút. Do đó để về nhà đúng giờ, bạn phải tăng tốc thêm \(2\;{\rm{km/h}}\). Tính vận tốc dự định và thời gian đi xe đạp của bạn Mai. Biết quãng đường lúc đi và lúc về đều là \(3\;{\rm{km}}\).
Quảng cáo
Trả lời:
Thời gian dự kiến bạn Mai đạp xe từ nhà ra Hồ Gươm và quay về nhà là \(\frac{6}{x}\) (giờ).
Thời gian Mai đạp xe từ nhà ra Hồ Gươm là \(\frac{3}{x}\) (giờ).
Vận tốc của bạn Mai khi đạp xe từ Hồ Gươm về nhà là \(x + 2\) (km/h).
Thời gian Mai đạp xe từ Hồ Gươm về nhà là \(\frac{3}{{x + 2}}\) (giờ).
Đổi \(3\) phút \( = \frac{1}{{20}}\) giờ.
Vì bạn Mai về nhà đúng giờ nên ta có phương trình \(\frac{3}{x} + \frac{3}{{x + 2}} + \frac{1}{{20}} = \frac{6}{x}\)
\( \Leftrightarrow \frac{1}{{20}} = \frac{6}{x} - \left( {\frac{3}{x} + \frac{3}{{x + 2}}} \right)\)
\( \Leftrightarrow \frac{1}{{20}} = \frac{3}{x} - \frac{3}{{x + 2}}\)
\( \Leftrightarrow \frac{1}{{60}} = \frac{1}{x} - \frac{1}{{x + 2}}\)
\[ \Leftrightarrow \frac{1}{{60}} = \frac{{x + 2}}{{x\left( {x + 2} \right)}} - \frac{x}{{x\left( {x + 2} \right)}}\]
\[ \Leftrightarrow \frac{1}{{60}} = \frac{{x + 2 - x}}{{x\left( {x + 2} \right)}}\]
\[ \Leftrightarrow \frac{1}{{60}} = \frac{2}{{x\left( {x + 2} \right)}}\]
\[ \Leftrightarrow x\left( {x + 2} \right) = 2.60\]
\[ \Leftrightarrow {x^2} + 2x - 120 = 0\]
\[ \Leftrightarrow {x^2} - 10x + 12x - 120 = 0\]
\[ \Leftrightarrow x\left( {x - 10} \right) + 12\left( {x - 10} \right) = 0\]
\[ \Leftrightarrow \left( {x + 12} \right)\left( {x - 10} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}x + 12 = 0\\x - 10 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = - 12\\x = 10\end{array} \right.\].
So với điều kiện, \(x = 10\) thỏa mãn.
Thời gian đi xe đạp của bạn Mai là \(\frac{3}{{10}} + \frac{3}{{10 + 2}} = \frac{{11}}{{20}}\) (giờ) \( = 33\) (phút).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
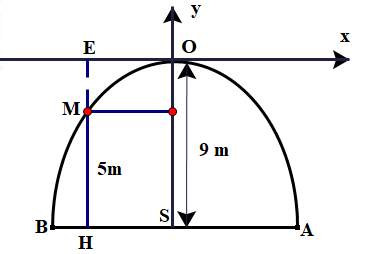
\({\rm{B}}( - 3; - 9) \in (P):y = a{x^2} \Rightarrow - 9 = a \cdot {( - 3)^2} \Rightarrow a = - 1\)
\((P):y = - {x^2}\)
Khi banh đạt độ cao 5 m thì \({\rm{ME}} = {\rm{HE}} - {\rm{HM}} = 9 - 5 = 4\;{\rm{m}}\)
\( \Rightarrow {\rm{M}}\left( {{x_M}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = - \sqrt 4 = - 2\)
Vậy sau 1 giây kể từ khi bóng được đá lên thì đạt độ cao 5 m.
Lời giải
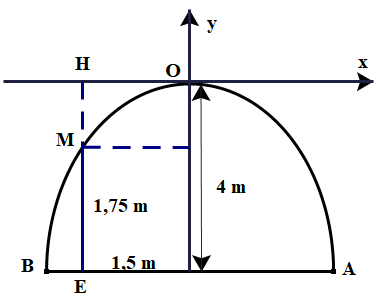
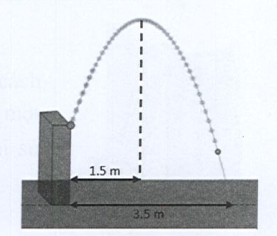
\({\rm{MH}} = {\rm{HE}} - {\rm{ME}} = 4 - 1,75 = 2,25\)
\( \Rightarrow {\rm{M}}( - 1,5; - 2,25) \in (P):y = a{x^2}\)\( \Rightarrow - 2,25 = a \cdot {( - 1,5)^2} \Rightarrow a = \frac{{ - 2,25}}{{{{( - 1,5)}^2}}} = - 1\)\((P):y = - {x^2}\)
\( \Rightarrow {\rm{A}}\left( {{x_A}; - 4} \right) \in (P):y = - {x^2} \Rightarrow - 4 = - x_{\rm{M}}^2 \Rightarrow x_{\rm{M}}^2 = 4 \Rightarrow {x_{\rm{M}}} = \sqrt 4 = 2\;{\rm{m}}\)
\({\rm{EA}} = {\rm{ES}} + {\rm{SA}} = 2 + 1,5 = 3,5\)
Vậy nước rơi xuống đất cách chân tháp một khoảng là \(3,5\;{\rm{m}}\).
Lời giải
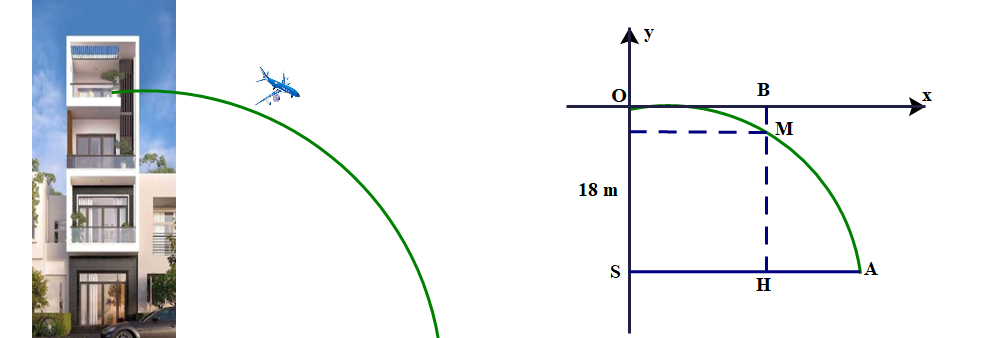
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
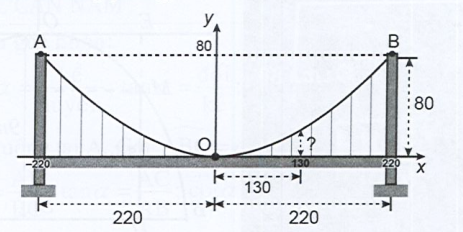
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.