khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 11
  3. Toán

Câu hỏi:

19/08/2025 1,517 Lưu

Một chiếc đu quay có bán kính \(75\;\,{\rm{m}}\), tâm của vòng quay ở độ cao \(90\;\,{\rm{m}}\), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?

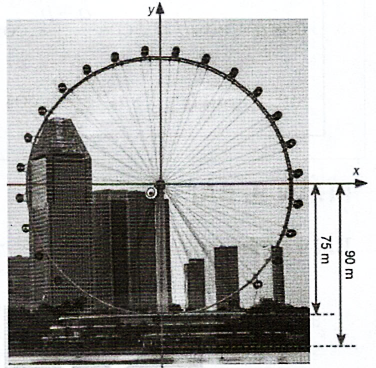
Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? (ảnh 1)

Xem lời giải

Câu hỏi trong đề: 22 câu Trắc nghiệm Toán 11 Cánh diều Bài 1. Góc lượng giác. Giá trị lượng giác của góc lượng giác (Đúng-sai, trả lời ngắn) có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

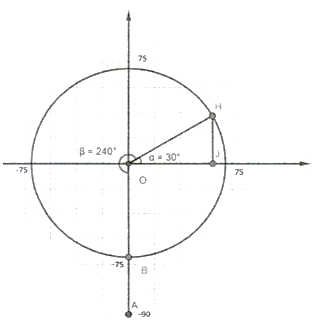
Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? (ảnh 2)

Do tính đối xứng, dù đu quay chuyển động theo chiều kim đồng hồ hay ngược chiều kim đồng hồ, ta đều thấy rằng độ cao của người đó là như nhau sau cùng một khoảng thời gian. Ở đây ta xét đu quay chuyển động theo chiều kim đồng hồ. Gắn đu quay có bán kính \(75\;\,{\rm{m}}\), tâm của vòng quay ở độ cao \(90\;\,{\rm{m}}\) vào hệ trục tọa độ \(Oxy\) ta được hình bên:

Sau 20 phút quay cabin đi được một góc là \(\frac{{20}}{{30}} \cdot 360^\circ = 240^\circ \) tức là đến vị trí điểm \(H\).

Khi đó \(\widehat {HOJ} = 30^\circ \) và \(HJ = OH\sin 30^\circ = 37,5\,\,{\rm{(m)}}\).

Vậy sau 20 phút quay, người đó ở độ cao \(37,5 + 90 = 127,5\,\,{\rm{(m)}}\).

Đáp án: 127,5.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút (đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy \(\pi = 3,14\)), biết rằng đường kính của bánh xe đạp là \(0,68\,\,{\rm{m}}\).

Lời giải

Chu vi bánh xe: \(C = \pi .d = 3,14.0,68\,\,{\rm{(m)}}\).

Trong 1 giây bánh xe quay được số vòng: \(\frac{{10}}{5} = 2\).

Số vòng bánh xe quay được trong 1 phút là: \(60.2 = 120\) (vòng).

Vậy quãng đường mà người đi xe đã đi được trong 1 phút là: \(S = 3,14.0,68.120 \approx 256\,\,{\rm{(m)}}\).

Đáp án: 256.

Câu 2

Biểu thức lượng giác \({\left[ {\sin \left( {\frac{\pi }{2} - x} \right) + \sin \left( {10\pi + x} \right)} \right]^2} + {\left[ {\cos \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {8\pi - x} \right)} \right]^2}\) có giá trị bằng?
A. \(1.\)                      
B. \(2.\)                    
C. \(\frac{1}{2}.\)          
D. \(\frac{3}{4}.\)

Lời giải

Đáp án đúng là: B

Ta có \(\sin \left( {\frac{\pi }{2} - x} \right) = \cos x;\) \(\sin \left( {10\pi  + x} \right) = \sin x.\)

Và \(\cos \left( {\frac{{3\pi }}{2} - x} \right) = \cos \left( {2\pi  - \frac{\pi }{2} - x} \right) = \cos \left( {\frac{\pi }{2} + x} \right) =  - {\mkern 1mu} \sin x;\) \(\cos \left( {8\pi  - x} \right) = \cos x.\)

Khi đó \({\left[ {\sin \left( {\frac{\pi }{2} - x} \right) + \sin \left( {10\pi  + x} \right)} \right]^{{\kern 1pt} 2}} + {\left[ {\cos \left( {\frac{{3\pi }}{2} - x} \right) + \cos \left( {8\pi  - x} \right)} \right]^{{\kern 1pt} 2}}\)

\( = {\left( {\cos x + \sin x} \right)^2} + {\left( {\cos x - \sin x} \right)^2}\)

\( = {\cos ^2}x + 2.\sin x.\cos x + {\sin ^2}x + {\cos ^2}x - 2.\sin x.\cos x + {\sin ^2}x = 2.\)

Câu 3

Biết \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) là các góc của tam giác \[ABC,\]mệnh đề nào sau đây đúng:
A. \(\sin \left( {A + C} \right) =  - {\mkern 1mu} \sin B.\)                                                             
B. \(\cos \left( {A + C} \right) =  - {\mkern 1mu} {\mkern 1mu} \cos B.\)
C. \(\tan \left( {A + C} \right) = \tan B.\)                                                             
D. \(\cot \left( {A + C} \right) = \cot B.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

a) Quãng đường vệ tinh \(X\) chuyển động được sau 1 giờ là: \[ \approx 28902,65\,\,{\rm{(km)}}{\rm{. }}\]

b) Quãng đường vệ tinh \(X\) chuyển động được sau 1,5 giờ là: \( \approx 43353,98\,\,{\rm{(km)}}\).

c) Sau khoảng 5,3 giờ thì \(X\) di chuyển được quãng đường \(240000\;\,{\rm{km}}\).

d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc \(\frac{{9\pi }}{2}\)rad?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho bốn cung (trên một đường tròn định hướng): \[\alpha  =  - \frac{{5\pi }}{6},\] \[\beta  = \frac{\pi }{{\rm{3}}}\], \[\gamma  = \frac{{{\rm{25}}\pi }}{{\rm{3}}},\] \[\delta  = \frac{{{\rm{19}}\pi }}{{\rm{6}}}\]. Các cung nào có điểm cuối trùng nhau?
A. \[\alpha \] và \[\beta \]; \[\gamma \] và \[\delta \].                               
B. \(\beta \) và \[\gamma \]; \[\alpha \] và \[\delta \].                            
C. \[\alpha ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma \].         
D. \[\beta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tính giá trị của \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right].\)
A. \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] =  - \frac{{\sqrt 3 }}{2}.\)                       
B. \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] =  - \frac{{\sqrt 2 }}{2}.\)
C. \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] =  - \frac{1}{2}.\)        
D. \(\cos \left[ {\frac{\pi }{4} + \left( {2k + 1} \right)\pi } \right] = \frac{{\sqrt 3 }}{2}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập