Câu hỏi:

19/08/2025 186

Cho hình chữ nhật ABCD có AB = 18cm và BC = 12cm. Trên AB lấy điểm M sao cho \(AM = \frac{1}{3}AB\) và trên BC lấy điểm N sao cho \(BN = \frac{1}{2}BC\). Tính diện tích hình tam giác DMN.

Xem lời giải

Câu hỏi trong đề: 16 bài tập Tam giác có lời giải !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

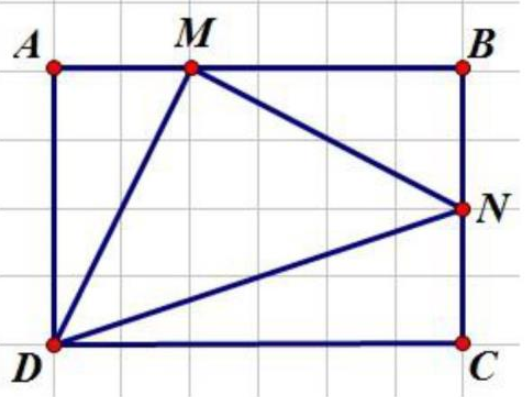
Tính diện tích hình tam giác DMN. (ảnh 1)

Ta có: \(AM = \frac{1}{3} \times AB = \frac{1}{3} \times 18 = 6(cm)\); BM = AB – AM = \(18 - 6 = 12(cm)\)

\(BN = CN = \frac{1}{2} \times BC = \frac{1}{2} \times 12 = 6(cm)\)

Từ đó ta tính được:

\({S_{DAM}} = \frac{1}{2} \times DA \times AM = \frac{1}{2} \times 12 \times 6 = 36(c{m^2})\)

\({S_{MBN}} = \frac{1}{2} \times MB \times BN = \frac{1}{2} \times 12 \times 6 = 36(c{m^2})\)

\({S_{DCN}} = \frac{1}{2} \times DC \times CN = \frac{1}{2} \times 18 \times 6 = 54(c{m^2})\)

\({S_{ABCD}} = AB \times BC = 18 \times 12 = 216(c{m^2})\)

Vậy:

\({S_{DMN}} = {S_{ABCD}} - ({S_{DAM}} + {S_{MBN}} + {S_{DCN}}) = 216 - (36 + 36 + 54) = 90(c{m^2})\)

Đáp Số: \(90(c{m^2})\)

Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chu vi tam giác: 54 cm. Chiều cao lần lượt là: 12 cm, 8cm, 6cm. Tính độ dài 3 cạnh hình tam giác?

Xem đáp án

Lời giải

Gọi độ dài 3 cạnh tam giác là: a, b, c tương ứng với các đường cao 12 cm, 8 cm, 6 cm.

Do chu vi là 54cm nên: \(a + b + c = 54(cm)\) \((1)\)

Lại có: \(\frac{1}{2} \times 12 \times a = \frac{1}{2} \times 8 \times b = \frac{1}{2} \times 6 \times c \to 6 \times a = 4 \times b = 3 \times c\)

Suy ra: \(b = \frac{3}{2} \times a\) và \(c = 2 \times a\). Thay vào (1) được:

\(a + \frac{3}{2} \times a + 2 \times a = 54 \to \frac{9}{2} \times a = 54 \to a = \frac{{54 \times 2}}{9} = 12\) cm

Từ đó: b = 18 cm và c = 24 cm

Đ/S: 12 cm; 18 cm và 24 cm.

Câu 2

Cho tam giác ABC. M, N lần lượt là trung điểm của AB và AC. Có MC và BN cắt nhau tại O. Tính diện tích tam giác MON biết diện tích tam giác ABC là \(132{m^2}\).

Xem đáp án

Lời giải

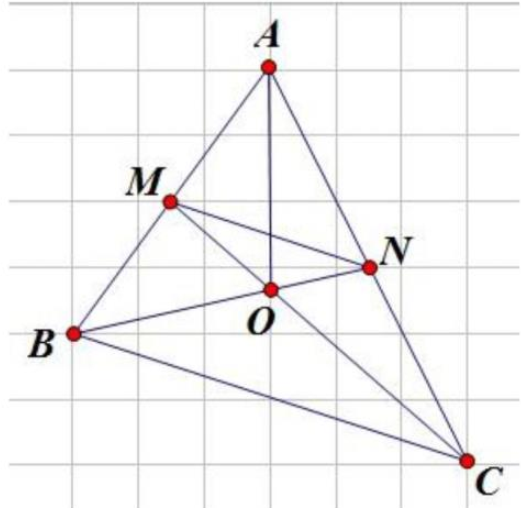
c (ảnh 1)

Nối A với O.

Ta có: \({S_{BCN}} = {S_{BAN}}\) (Vì cùng bằng \(\frac{1}{2} \times {S_{ABC}}\)) mà hai tam giác này chung đáy BN.

\( \Rightarrow \) Chiều cao hạ từ C xuống BN = chiều cao hạ từ A xuống BN.

\( \Rightarrow {S_{CBO}} = {S_{ABO}}\) (chung đáy BO và chiều cao bằng nhau) (1)

Lại có: \({S_{CBM}} = {S_{CAM}}\) (Vì cùng bằng \(\frac{1}{2} \times {S_{ABC}}\)) mà hai tam giác này chung đáy CM.

\( \Rightarrow \) Chiều cao hạ từ B xuống CM = chiều cao hạ từ A xuống CM.

\( \Rightarrow {S_{CBO}} = {S_{ACO}}\) (chung đáy CO và chiều cao bằng nhau) (2)

Từ (1) và (2) có: \({S_{OAB}} = {S_{OAC}} = {S_{OBC}} = \frac{1}{3} \times {S_{ABC}} = \frac{1}{3} \times 132 = 44(c{m^2})\)

Ta có: \({S_{OBM}} = \frac{1}{2} \times {S_{OAB}} = 22(c{m^2})\); \({S_{OCN}} = \frac{1}{2} \times {S_{OAC}} = 22(c{m^2})\)

Cũng có: \({S_{AMN}} = \frac{1}{2} \times {S_{NAB}} = \frac{1}{2} \times \frac{1}{2} \times {S_{ABC}} = 33(c{m^2})\).

Mặt khác: \({S_{OAB}} + {S_{OAC}} = {S_{OBM}} + {S_{OCN}} + {S_{AMN}} + {S_{OMN}}\)

\( \to {S_{OMN}} = ({S_{OAB}} + {S_{OAC}}) - ({S_{OBM}} + {S_{OCN}} + {S_{AMN}})\)

Thay số được:

\({S_{OMN}} = (44 + 44) - (22 + 22 + 33) = 11(c{m^2})\)

Vậy \({S_{OMN}} = 11(c{m^2})\)

Đáp Số: 11 \(c{m^2}\).

Câu 3