11 bài tập Hình thang có lời giải

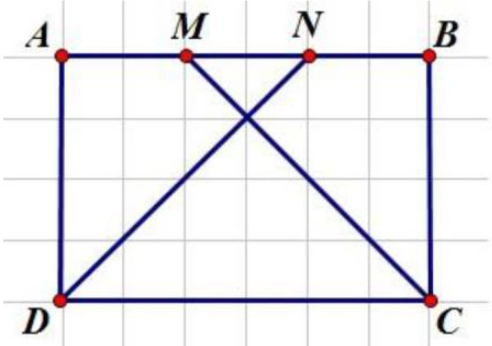
a) Ta có: \({S_{AMCD}} = \frac{{(AM + CD) \times AD}}{2}\) và \({S_{NBCD}} = \frac{{(BN + CD) \times BC}}{2}\)

Mà AM = BN và AD = BC nên \({S_{AMCD}} = {S_{NBCD}} \to \frac{{{S_{AMCD}}}}{{{S_{NBCD}}}} = 1\).

b) Theo đề bài ta có: \(AM = \frac{1}{3} \times AB\)

\( \to {S_{AMCD}} = \frac{{(AM + CD) \times AD}}{2} = \frac{{\left( {\frac{1}{3} \times AB + AB} \right) \times AD}}{2} = \frac{2}{3} \times AB \times AD = \frac{2}{3} \times {S_{ABCD}}\)

Vậy \(\frac{{{S_{AMCD}}}}{{{S_{ABCD}}}} = \frac{2}{3}\)

Đáp Số: a) 1                    b) \(\frac{2}{3}\)

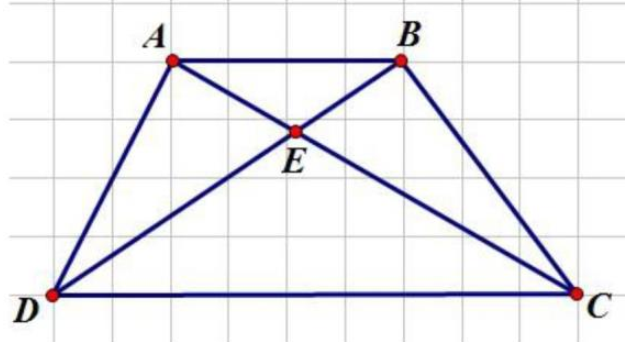
Ta có:

\({S_{ACD}} = {S_{BCD}}\) (chung đáy CD và chiều cao tương ứng bằng chiều cao hình thang ABCD)

\({S_{DAB}} = {S_{CAB}}\) (chung đáy AB và chiều cao tương ứng bằng chiều cao hình thang ABCD)

Lại có: \({S_{ACD}} = {S_{EAD}} + {S_{ECD}}\) và \({S_{BCD}} = {S_{EBC}} + {S_{ECD}}\). Suy ra: \({S_{EAD}} = {S_{EBC}}\).

Vậy các cặp tam giác bằng nhau là: \({S_{ACD}} = {S_{BCD}}\); \({S_{DAB}} = {S_{CAB}}\); \({S_{EAD}} = {S_{EBC}}\)

Đáp Số: \({S_{ACD}} = {S_{BCD}}\); \({S_{DAB}} = {S_{CAB}}\); \({S_{EAD}} = {S_{EBC}}\)

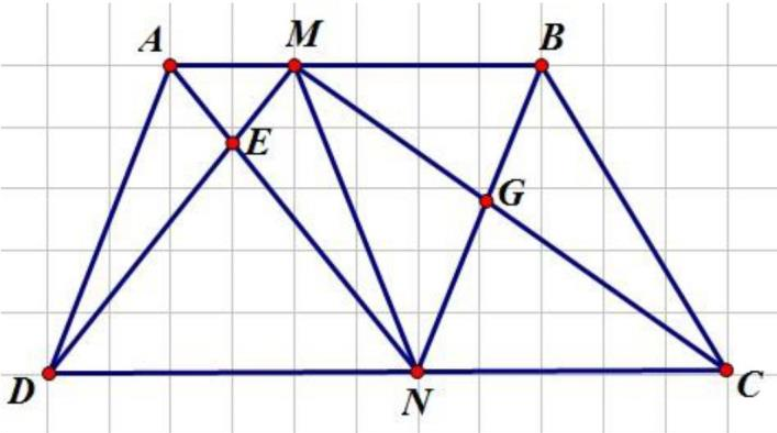
Nối M với N. Ta có: AMND và BMNC là hai hình thang.

Tương tự bài 2, trong hai hình thang AMND và BMNC ta lần lượt có được:

\({S_{AED}} = {S_{EMN}}\) và \({S_{BGC}} = {S_{GMN}} \Rightarrow {S_{EMN}} + {S_{GMN}} = {S_{AED}} + {S_{BGC}}\)

Mà \({S_{EMN}} + {S_{GMN}} = {S_{MGNE}}\).

Do đó: \({S_{MGNE}} = {S_{AED}} + {S_{BGC}} = 1,2 + 3,4 = 4,6(c{m^2})\)

Đáp Số: 4,6 (\(c{m^2}\)).

Nối A với E; Nối A với C; Nối E với N; Nối N với C.

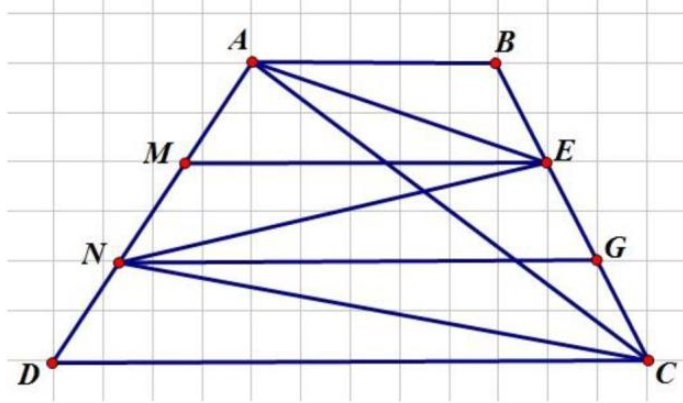
Ta có:

\({S_{ABE}} = \frac{1}{3} \times {S_{ABC}}\) (chung chiều cao hạ từ A xuống BC và \(BE = \frac{1}{3} \times BC\))

\({S_{CDN}} = \frac{1}{3} \times {S_{ACD}}\) (chung chiều cao hạ từ C xuống DC và \(ND = \frac{1}{3} \times AD\))

Lại có: \({S_{ABC}} + {S_{ACD}} = {S_{ABCD}}\). Suy ra: \({S_{ABE}} + {S_{CDN}} = \frac{1}{3} \times {S_{ABCD}}\).

Cũng có: \({S_{ABE}} + {S_{AEM}} + {S_{EMN}} + {S_{EGN}} + {S_{CGN}} + {S_{CDN}} = {S_{ABCD}}\).

Suy ra: \({S_{AEM}} + {S_{EMN}} + {S_{EGN}} + {S_{CGN}} = \frac{2}{3} \times {S_{ABCD}}\). (1)

Mặt khác có:

\({S_{AEM}} = {S_{EMN}}\) (chung chiều cao hạ từ E xuống AD và AM = MN)

\({S_{EGN}} = {S_{CGN}}\) (chung chiều cao hạ từ N xuống BC và EG = GC)

Do đó: \({S_{AEM}} + {S_{CGN}} = {S_{EMN}} + {S_{EGN}}\) (2)

Từ (1) và (2) có: \({S_{EMN}} + {S_{EGN}} = \frac{1}{3} \times {S_{ABCD}}\)

Hay \({S_{MEGN}} = \frac{1}{3} \times {S_{ABCD}} = \frac{1}{3} \times 108 = 36(c{m^2})\)

Đáp Số: 36 (\(c{m^2}\))

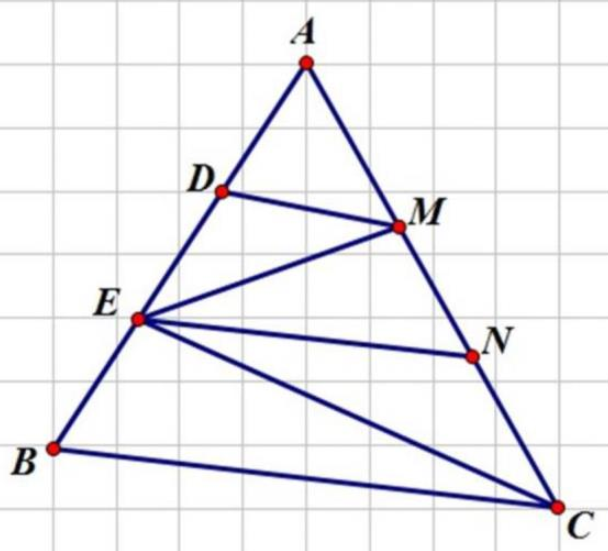
Ta có: \({S_{MAD}} = {S_{MED}}\) (Chung chiều cao hạ từ M xuống AB và AD = DE)

\({S_{EMN}} = {S_{ECN}}\) (chung chiều cao hạ từ E xuống AC và MN = CN)

Do đó: \({S_{MAD}} + {S_{ECN}} = {S_{MED}} + {S_{EMN}} = {S_{DMNE}}\) (1)

Lại có: \({S_{ACE}} = {S_{MAD}} + {S_{ECN}} + {S_{MED}} + {S_{EMN}}\) (2)

Từ (1) và (2) có: \({S_{DMNE}} = \frac{1}{2} \times {S_{ACE}}\) (3)

Cũng có: \({S_{ACE}} = \frac{2}{3} \times {S_{ABC}}\) (chung chiều cao hạ từ C xuống AB và \(AE = \frac{2}{3} \times AB\)) \( \to {S_{ABC}} = \frac{3}{2} \times {S_{ACE}}\) (4)

Từ (3) và (4) có: \({S_{DMNE}} = \frac{1}{2} \times \frac{3}{2} \times {S_{ABC}} = \frac{3}{4} \times {S_{ABC}} \to {S_{ABC}} = \frac{4}{3} \times {S_{DMNE}}\)

Do đó: \({S_{ABC}} = \frac{4}{3} \times 12 = 16(c{m^2})\)

Đáp Số: 16 \(c{m^2}\).