14 bài tập Giải toán liên quan đến tỉ lệ diện tích tam giác có lời giải

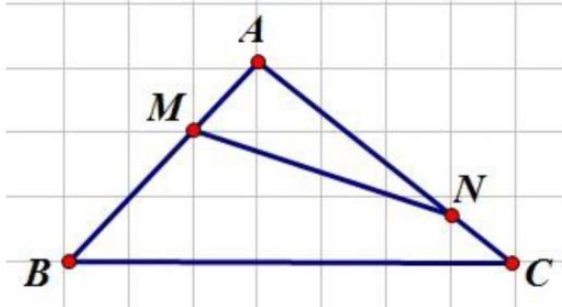
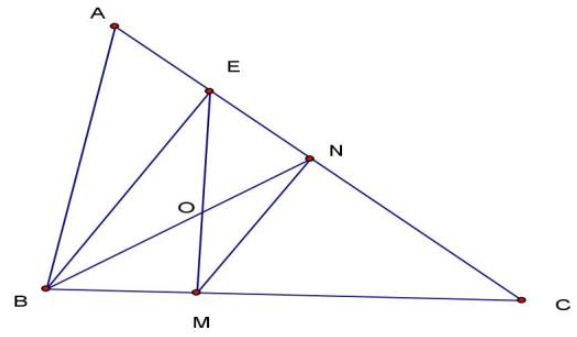
\({S_{MBCN}} = {S_{BMN}} + {S_{BCN}} = \frac{2}{3} \times {S_{NAB}} + \frac{1}{4} \times {S_{ABC}}\)

\( = \frac{2}{3} \times \frac{3}{4} \times {S_{ABC}} + \frac{1}{4} \times {S_{ABC}} = \frac{3}{4} \times {S_{ABC}} = 180{\rm{ c}}{{\rm{m}}^2}\)

\({S_{ABC}} = 180 \times 4:3 = 240{\rm{ c}}{{\rm{m}}^2}\).

Đáp Số: \(240{\rm{ c}}{{\rm{m}}^2}\)

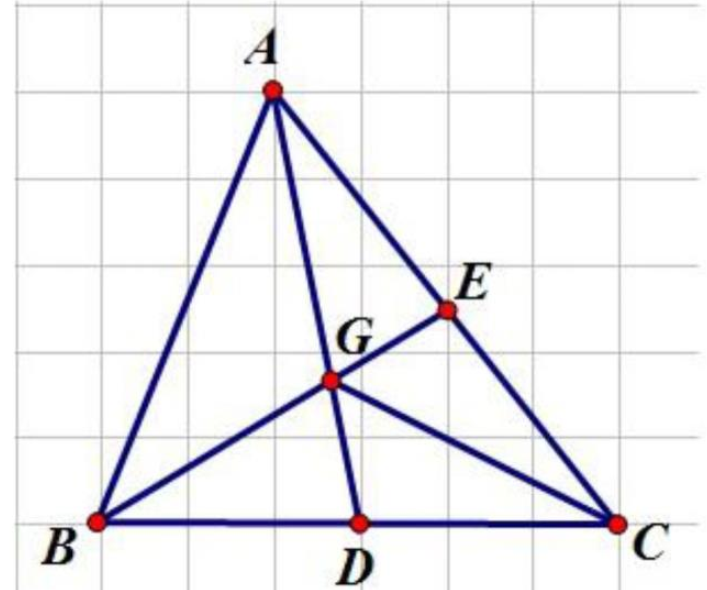
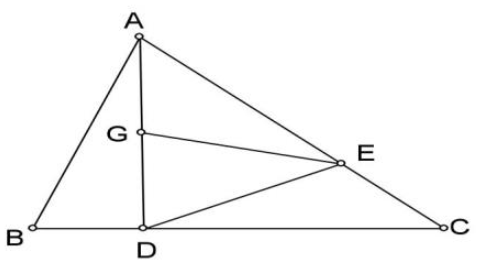
Nối C với G.

Ta có: \({S_{BCE}} = {S_{ACD}}\) (Vì cùng bằng \(\frac{1}{2}{S_{ABC}}\))

Mà: \({S_{BCE}} = {S_{GBD}} + {S_{CDGE}}\) và \({S_{ACD}} = {S_{GAE}} + {S_{CDGE}}\)

\( \Rightarrow {S_{GBD}} = {S_{GAE}} = \frac{1}{2}{S_{GAC}}\) (1)

Cũng có: \({S_{GBD}} = {S_{GCD}}\) (chung chiều cao hạ từ G, đáy \(BD = CD\)) (2)

Từ (1) và (2) suy ra: \({S_{GCD}} = \frac{1}{2}{S_{GAC}}\) mà hai tam giác này chung chiều cao hạ từ C nên: \(GD = \frac{1}{2}GA\) hay GA gấp đôi GD. (đpcm)

Đáp Số: gấp đôi.

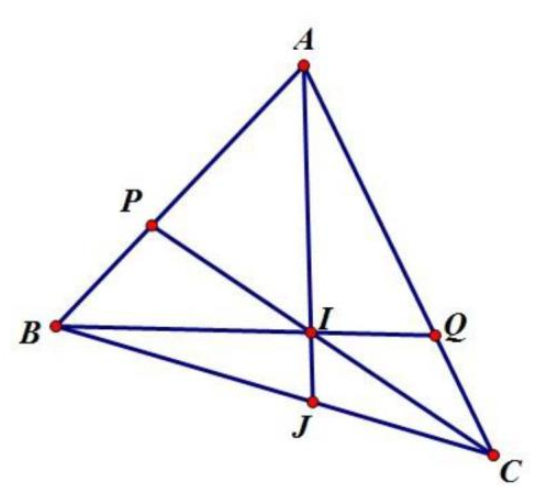
Vì \(BP = \frac{1}{2}PA;CQ = \frac{1}{3}QA\) nên có:

\({S_{IAP}} = 2 \times {S_{IBP}}\); \({S_{IAQ}} = 3 \times {S_{ICQ}}\);

\({S_{IAP}} + {S_{IAQ}} + {S_{IBQ}} = \frac{2}{3} \times {S_{ABC}}\)

\({S_{IBP}} + {S_{IAP}} + {S_{IAQ}} = \frac{3}{4} \times {S_{ABC}}\)

Từ đó có được:

\({S_{IBP}} = \frac{1}{6} \times {S_{ABC}};{S_{IAP}} = \frac{1}{3} \times {S_{ABC}};{S_{IAQ}} = \frac{1}{4} \times {S_{ABC}};{S_{ICQ}} = \frac{1}{{12}} \times {S_{ABC}}\)

Vậy: \(\frac{{BJ}}{{JC}} = \frac{{{S_{IBJ}}}}{{{S_{ICJ}}}} = \frac{{{S_{IAP}} + {S_{IBP}} + {S_{IBJ}}}}{{{S_{IAQ}} + {S_{ICQ}} + {S_{ICJ}}}} = \frac{{{S_{IAP}} + {S_{IBP}}}}{{{S_{IAQ}} + {S_{ICQ}}}} = \frac{{\frac{1}{3} \times {S_{ABC}} + \frac{1}{6} \times {S_{ABC}}}}{{\frac{1}{4} \times {S_{ABC}} + \frac{1}{{12}} \times {S_{ABC}}}} = \frac{{\frac{1}{2}}}{{\frac{1}{3}}} = \frac{3}{2}\)

Đáp Số: \(\frac{{BJ}}{{JC}} = \frac{3}{2}\)

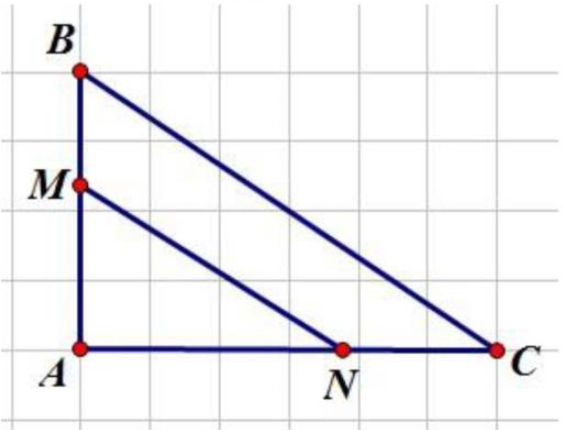
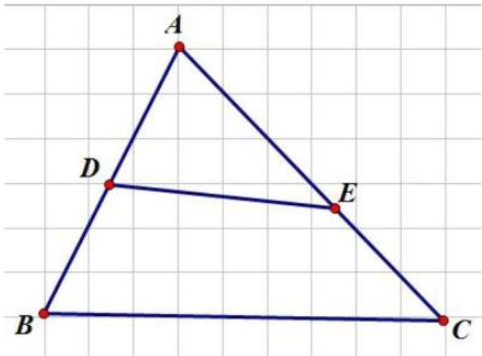
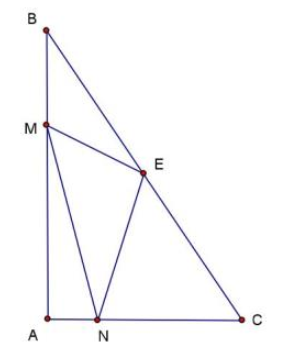
Vì \(MN//BC \Rightarrow MNBC\) là hình thang.

Nối BN, CM

\({S_{BCM}} = \frac{1}{3}{S_{ABC}}\) (\(BM = 30 - 20 = 10{\rm{ cm, }}\frac{{BM}}{{AB}} = \frac{{10}}{{30}} = \frac{1}{3}\), chung chiều cao hạ từ C)

\({S_{BMC}} = {S_{BNC}}\) (chung đáy BC, chiều cao là chiều cao hình thang MNBC)

Mà \({S_{ABC}} = 30 \times 45:2 = 675{\rm{ c}}{{\rm{m}}^2}\)

\( \Rightarrow {S_{BNC}} = 675 \times \frac{1}{3} = 225{\rm{ c}}{{\rm{m}}^2}\)

Độ dài NC = \(225 \times 2:30 = 15{\rm{ cm}}\)

Độ dài AN = \(45 - 15 = 30{\rm{ cm}}\)

\({S_{AMN}} = 30 \times 20:2 = 300{\rm{ c}}{{\rm{m}}^2}\)

Đáp Số: \(300{\rm{ c}}{{\rm{m}}^2}\).

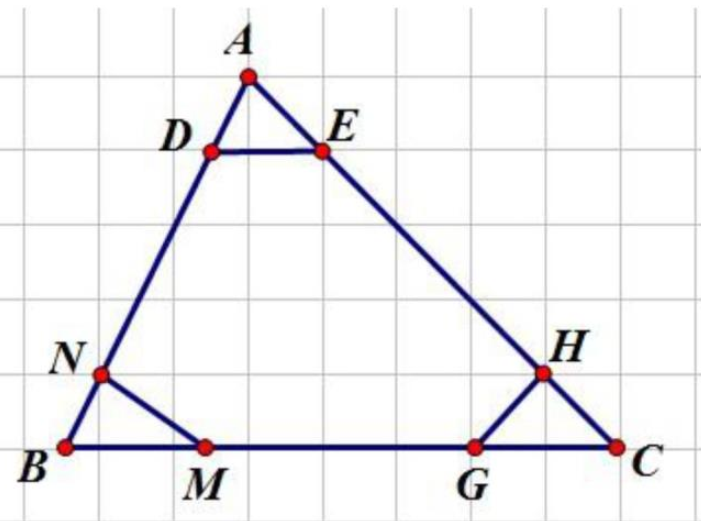
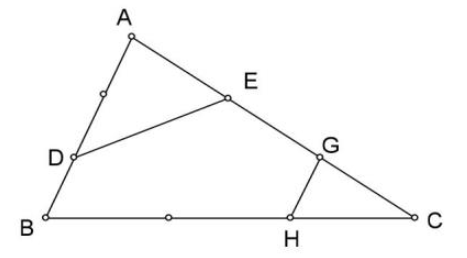
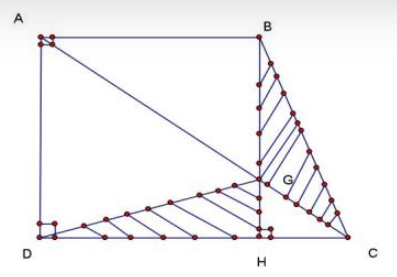
a) Nối B với E.

Có: \({S_{ABE}} = \frac{1}{5} \times {S_{ABC}}\) (Do chung chiều cao hạ từ B và \(AE = \frac{1}{5}AC\))

Và \({S_{ADE}} = \frac{1}{5} \times {S_{ABE}}\) (Do chung chiều cao hạ từ E và \(AD = \frac{1}{5}AB\))

Do đó: \({S_{ADE}} = \frac{1}{{25}} \times {S_{ABC}}\)

b/ Tương tự phần a tính được: \({S_{BMN}} = {S_{CGH}} = \frac{1}{{25}} \times {S_{ABC}}\)

Suy ra: \({S_{ADE}} + {S_{BMN}} + {S_{CGH}} = \frac{3}{{25}} \times {S_{ABC}}\)

Suy ra: \({S_{DEHGMN}} = {S_{ABC}} - \frac{3}{{25}} \times {S_{ABC}} = \frac{{22}}{{25}} \times {S_{ABC}}\)

\({S_{ADE}} = \frac{1}{2} \times {S_{EAB}} = \frac{1}{2} \times \frac{2}{3} \times {S_{ABC}} = \frac{1}{3} \times {S_{ABC}} = \frac{1}{3} \times 180 = 60(c{m^2})\)

Đáp Số: 60 cm²