Cho hình chữ nhật ABCD có AB = 4,5cm; BC = 3cm. Chia hình đó thành hình vuông AEGD và hình chữ nhật EBCG. Nối D với E. Đường chéo AC cắt DE ở M và cắt EG ở N. Tính diện tích hình tam giác NDC.
Cho hình chữ nhật ABCD có AB = 4,5cm; BC = 3cm. Chia hình đó thành hình vuông AEGD và hình chữ nhật EBCG. Nối D với E. Đường chéo AC cắt DE ở M và cắt EG ở N. Tính diện tích hình tam giác NDC.
Câu hỏi trong đề: 11 bài tập Hình thang có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nối A với G.
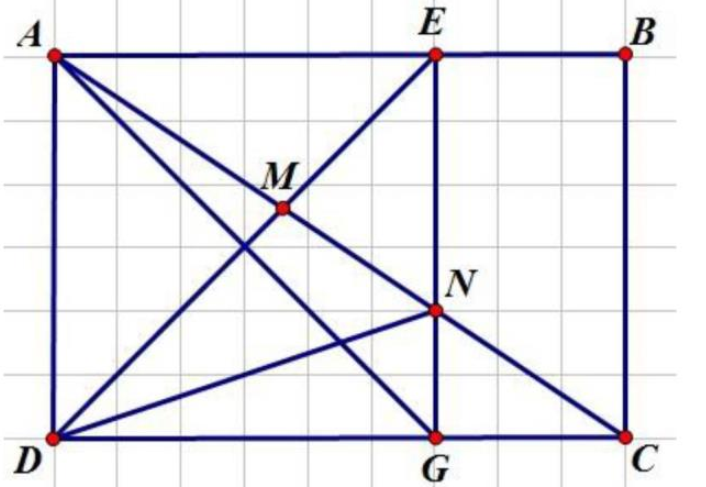
Ta có: \({S_{ANG}} = {S_{DNG}}\) (chung đáy NG, chiều cao hạ từ A và D của 2 tam giác xuống NG bằng AE)
\( \Rightarrow {S_{ANG}} + {S_{CNG}} = {S_{DNG}} + {S_{CNG}} \Rightarrow {S_{ACG}} = {S_{NDC}}\).
Lại có: GC = DC - DG = DC - AD = 4,5 – 3 = 1,5 (cm)
Suy ra: \({S_{ACG}} = \frac{1}{2} \times AD \times GC = \frac{1}{2} \times 3 \times 1,5 = 2,25(c{m^2})\)
Vậy: \({S_{NDC}} = 2,25(c{m^2})\)
Đáp Số: 2,25 \(c{m^2}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
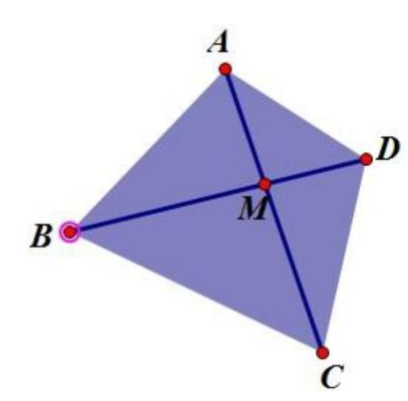
Ta có:
\({S_{ABC}} = {S_{DBC}} = 10 \times 12:2 = 60{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
\({S_{ABD}} = {S_{ACD}} = 20 \times 12:2 = 120{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\) (1)
Từ (1) Suy ra: \({S_{MAB}} = {S_{MCD}}\).
Vì hai tam giác ABD và CBD có chung đáy BD mà \({S_{CBD}} = \frac{1}{2}{S_{ABD}}\). Suy ra, đường cao hạ từ A tới BD gấp 2 lần đường cao hạ từ C tới BD. (2)
Xét hai tam giác MDA và MCD có chung đáy DM và do (2) suy ra:
\({S_{MCD}} = \frac{1}{2}{S_{MDA}} = \frac{1}{3}{S_{ACD}} = 120:3 = 40{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\).
Vậy \({S_{MDA}} = 120 - 40 = 80{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\); \({S_{MBC}} = 60 - 40 = 20{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \({S_{MCD}} = 40{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\). \({S_{MDA}} = 80{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\); \({S_{MBC}} = 20{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Lời giải
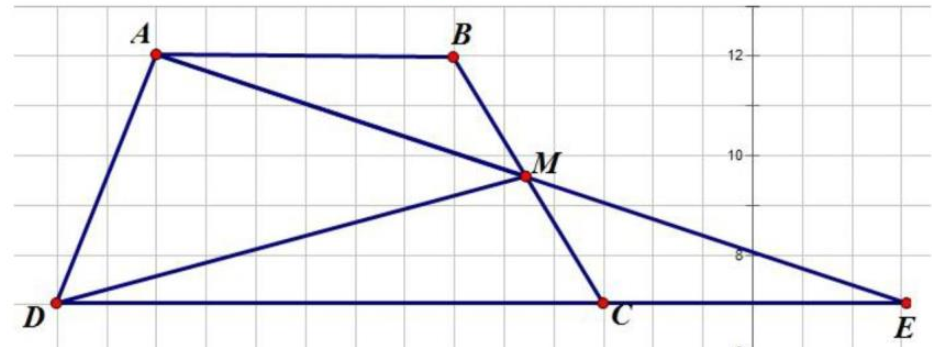
Cắt hình tam giác ABM rồi ghép hình được tam giác ADE.
Do đó: \({S_{ABCD}} = {S_{ADE}} = {S_{AMD}} + {S_{MDE}}\).
Có: \({S_{AMD}} = {S_{MDE}}\) (vì AM = ME và chung chiều cao hạ từ D xuống AE)
Do đó: \({S_{MDE}} = 12,5(c{m^2})\)
Vậy \({S_{ABCD}} = 12,5 + 12,5 = 25(c{m^2})\)
Đáp Số: 25 \(c{m^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo