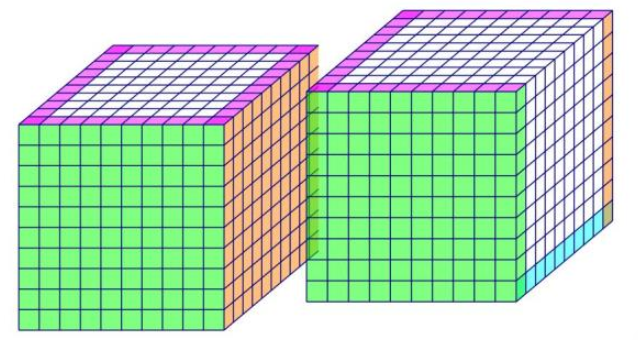
Xếp các hình lập phương nhỏ cạnh 1 cm thành một hình hộp chữ nhật có các kích thước là 1,6 dm; 1,2 dm; 8 cm. Sau đó người ta sơn tất cả 6 mặt vừa xếp được. Tính số hình lập phương nhỏ được sơn 3 mặt, 2 mặt, 1 mặt, không được sơn mặt nào.

Hình lập phương lớn có cạnh là 10cm (vì \(10 \times 10 \times 10 = 1000\))

Trường hợp 1: Sơn 4 mặt bên.

Hình hình lập phương nhỏ không sơn mặt nào tạo thành khối hình hộp chữ nhật có 3 kích thước: \(8 \times 8 \times 10 = 640\) (hình)

Trường hợp 2: Sơn 3 mặt bên và 1 mặt đáy.

Hình hình lập phương nhỏ không sơn mặt nào tạo thành khối hình hộp chữ nhật có 3 kích thước: \(8 \times 9 \times 9 = 648\) (hình)

Đáp số: 648 hình

Vì \(125 = 5\) nên các đường sẽ chia mỗi cạnh của hình lập phương thành 5 phần bằng nhau.

Các hình lập phương nhỏ nằm ở 8 góc của hình lập phương to sẽ có 3 mặt được sơn đen nên số các hình này là 8 hình.

Các hình lập phương nhỏ có cạnh nằm trên cạnh hình lập phương nhưng không chứa đỉnh của hình lập phương to sẽ đúng có 2 mặt được sơn đen.

Do đó số các hình này là: \(12 \times (5 - 2) = 36\) (hình)

Các hình lập phương nhỏ có một mặt thuộc mặt của hình lập phương lớn nhưng không chứa đỉnh và cạnh của hình lập phương to sẽ đúng có 1 mặt được sơn đen. Do đó số hình này có là: \(6 \times (3 \times 3) = 54\) (hình)

Còn lại số hình lập phương nhỏ không có mặt nào bị sơn đen là:

\(125 - (8 + 36 + 54) = 27\) (hình).