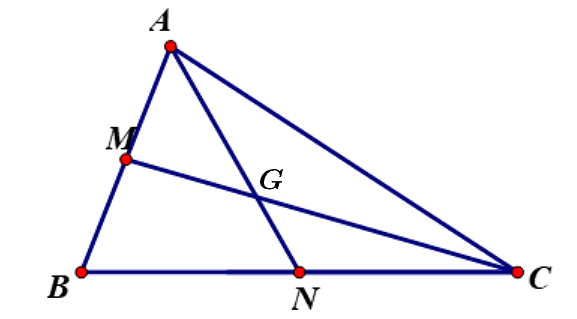
Gọi \[AN,{\rm{ }}CM\] là các đường trung tuyến của tam giác \[ABC\] và G là trọng tâm.

a) \[\overrightarrow {AN}  = \overrightarrow {AB}  + \overrightarrow {AC} \,.\]

b) \[\overrightarrow {CM}  = \frac{3}{2}\overrightarrow {GC} \,.\]

c) \[\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {BC}  - \overrightarrow {BA} } \right)\,.\]

d) \[\overrightarrow {AB}  = \frac{4}{3}\overrightarrow {AN}  + \frac{2}{3}\overrightarrow {CM} \].

a) Sai. Theo tính chất trung điểm đoạn thẳng BC ta có \[\overrightarrow {AN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\].

b) Sai. Vì G là trọng tâm tam giác \[ABC\] nên \[\overrightarrow {CM}  = \frac{3}{2}\overrightarrow {CG} \].

c) Đúng. Do M, N lần lượt là trung điểm của cạnh AB và BC nên MN là đường trung bình của tam giác \[ABC\], do đó ta có \[\overrightarrow {MN}  = \frac{1}{2}\overrightarrow {AC}  = \frac{1}{2}\left( {\overrightarrow {BC}  - \overrightarrow {BA} } \right)\].

d) Đúng. Ta có \[\overrightarrow {AN}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \frac{1}{2}\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AC} \];

\[\overrightarrow {CM}  = \overrightarrow {CA}  + \overrightarrow {AM}  \Rightarrow \frac{1}{2}\overrightarrow {CM}  = \frac{1}{2}\overrightarrow {CA}  + \frac{1}{2}\overrightarrow {AM} \].

Suy ra

\[\overrightarrow {AN}  + \frac{1}{2}\overrightarrow {CM}  = \frac{1}{2}\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AC}  + \frac{1}{2}\overrightarrow {CA}  + \frac{1}{2}\overrightarrow {AM}  = \frac{1}{2}\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AC}  - \frac{1}{2}\overrightarrow {AC}  + \frac{1}{2} \cdot \frac{1}{2}\overrightarrow {AB}  = \frac{3}{4}\overrightarrow {AB} \].

Do đó \[\overrightarrow {AB}  = \frac{4}{3}\overrightarrow {AN}  + \frac{2}{3}\overrightarrow {CM} \].