Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.

c) Nếu hàm chi phí hằng tuần là \(C\left( x \right) = 12000 - 3x\) (triệu đồng), trong đó \(x\) là số ti vi bán ra trong tuần, vậy có \[2300\] ti vi được bán ra thì lợi nhuận là cao nhất.

c) Sai: Doanh thu bán hàng của \(x\) sản phẩm là: \(R\left( x \right) = x.p\left( x \right) = x.\left( {\frac{{ - 1}}{{200}}x + 19} \right) = \frac{{ - {x^2}}}{{200}} + 19x\) (triệu đồng). Do đó, hàm số thể hiện lợi nhuận thu được khi bán \[x\] sản phẩm là:

\(P\left( x \right) = R\left( x \right) - C\left( x \right) = \frac{{ - {x^2}}}{{200}} + 19x - 12000 + 3x = \frac{{ - {x^2}}}{{200}} + 22x - 12000\) (triệu đồng).

Để lợi nhuận là lớn nhất thì \[P\left( x \right)\] là lớn nhất. Ta có: \(P'\left( x \right) = \frac{{ - x}}{{100}} + 22;\,\,\,P'\left( x \right) = 0 \Leftrightarrow x = 2200\)

Bảng biến thiên:

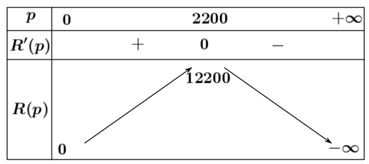
Vậy có \[2200\] ti vi được bán ra thì lợi nhuận là cao nhất.

Số ti vi mua tăng lên là: \(2200 - 1000 = 1200\) (chiếc)