Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(M{A^2} = M{B^2} + M{C^2}\) người ta cắt bỏ bốn tam giác cân bằng nhau là \(AMB\), \(BNC\), \(CPD\) và \(DQA\). Với phần còn lại người ta gấp lên và ghép lại để thành hình chóp tứ giác đều.
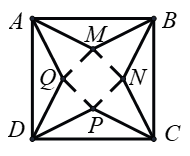
Gọi cạnh đáy của mô hình là \(x\) (cm) với \(x > 0\).
a) Chiều cao của hình chóp là \(\sqrt {1250 - 25\sqrt 2 x} \).
Từ một tấm bìa hình vuông \(ABCD\) có cạnh bằng \(M{A^2} = M{B^2} + M{C^2}\) người ta cắt bỏ bốn tam giác cân bằng nhau là \(AMB\), \(BNC\), \(CPD\) và \(DQA\). Với phần còn lại người ta gấp lên và ghép lại để thành hình chóp tứ giác đều.
Gọi cạnh đáy của mô hình là \(x\) (cm) với \(x > 0\).
a) Chiều cao của hình chóp là \(\sqrt {1250 - 25\sqrt 2 x} \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
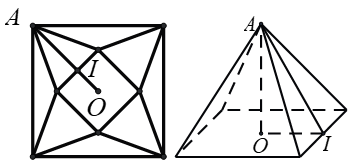
a) Đúng : Gọi cạnh đáy của mô hình là \(x\) (cm) với \(x > 0\). Ta có \(AI = AO - IO\)\( = 25\sqrt[{}]{2} - \frac{x}{2}\).
Chiều cao của hình chóp \(h = \sqrt {A{I^2} - O{I^2}} = \sqrt {{{\left( {25\sqrt[{}]{2} - \frac{x}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}\,} = \sqrt[{}]{{1250 - 25\sqrt[{}]{2}x}}\).
Câu hỏi cùng đoạn
Câu 2:
b) Điều kiện của \(x\) là: \(0 < x < 25\sqrt 2 \)
Lời giải của GV VietJack
b) Đúng: Điều kiện \(1250 - 25\sqrt[{}]{2}x > 0\)\( \Rightarrow x < 25\sqrt[{}]{2}\).
Câu 3:
c) Thể tích của khối chóp bằng \[\frac{1}{3}.\sqrt[{}]{{1250{x^3} - 25\sqrt[{}]{2}{x^4}}}\].
c) Thể tích của khối chóp bằng \[\frac{1}{3}.\sqrt[{}]{{1250{x^3} - 25\sqrt[{}]{2}{x^4}}}\].
Lời giải của GV VietJack
c) Sai: Thể tích của khối chóp bằng \[V = \frac{1}{3}.{x^2}.\sqrt[{}]{{1250 - 25\sqrt[{}]{2}x}}\]\[ = \frac{1}{3}.\sqrt[{}]{{1250{x^4} - 25\sqrt[{}]{2}{x^5}}}\].
Câu 4:
d) Khi cạnh đáy của khối chóp bằng \(3\sqrt 2 {\rm{dm}}\) thì thể tích của khối chóp là lớn nhất
d) Khi cạnh đáy của khối chóp bằng \(3\sqrt 2 {\rm{dm}}\) thì thể tích của khối chóp là lớn nhất
Lời giải của GV VietJack
d) Sai: Xét hàm số \[y = \frac{1}{3}.\sqrt[{}]{{1250{x^4} - 25\sqrt[{}]{2}{x^5}}}\] với \(0 < x < 25\sqrt[{}]{2}\).
Ta có \(y' = \frac{1}{3}.\frac{{5000{x^3} - 125\sqrt[{}]{2}{x^4}}}{{2\sqrt[{}]{{1250{x^4} - 25\sqrt[{}]{2}{x^3}}}}}\); \[y' = 0\]\( \Rightarrow 5000{x^3} - 125\sqrt[{}]{2}{x^4} = 0\)\( \Rightarrow x = 20\sqrt[{}]{2}\).
Bảng biến thiên
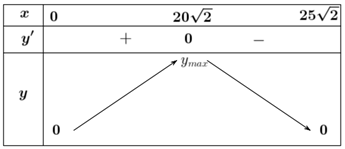
Vậy để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình bằng \(20\sqrt[{}]{2}\,{\rm{cm}}\)\( = 2\sqrt[{}]{2}\,{\rm{dm}}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng: Vào đầu năm 1980, ta có \(t = 10;f\left( {10} \right) = 18\). Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
Vào đầu năm 1995 ta có \(t = 25;f\left( {25} \right) = 22\).
Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.
Lời giải
a) Sai : Do \(x\) là độ dài của đoạn dây cuộn thành hình tròn \(\left( {0 < x < a} \right)\).
Suy ra chiều dài đoạn còn lại là \(a - x\).
Chu vi đường tròn: \(2\pi r = x\)\( \Rightarrow r = \frac{x}{{2\pi }}\). Diện tích hình tròn: \({S_1} = \pi .{r^2}\)\( = \frac{{{x^{\rm{2}}}}}{{4\pi }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo