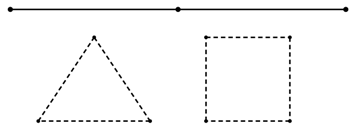
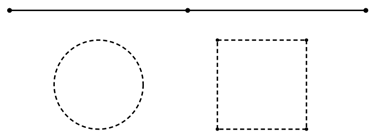
Một tấm bìa hình vuông có diện tích \(900\,{\rm{c}}{{\rm{m}}^2}\). Người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) cm rồi gập tấm bìa lại như hình vẽ bên để được một cái hộp không nắp có dạng hình hộp chữ nhật. Tìm thể tích lớn nhất mà hình hộp chữ nhật có thể thu được?
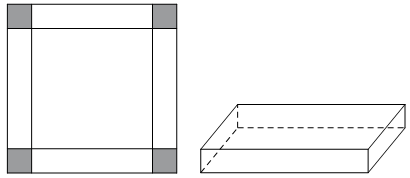
Một tấm bìa hình vuông có diện tích \(900\,{\rm{c}}{{\rm{m}}^2}\). Người ta cắt ở bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) cm rồi gập tấm bìa lại như hình vẽ bên để được một cái hộp không nắp có dạng hình hộp chữ nhật. Tìm thể tích lớn nhất mà hình hộp chữ nhật có thể thu được?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cạnh của tấm bìa là \[a = \sqrt S = \sqrt {900} = 30\,\,{\rm{cm}}\], đáy sẽ là hình vuông có cạnh bằng \(30 - 2x\).
Thể tích thu được là: \(V = {\left( {30 - 2x} \right)^2}x = f\left( x \right)\) với \(0 \le x \le \frac{a}{1} = 15\)
Dễ dàng tính được: \({V_{{\rm{max}}}} = \max f\left( x \right) = f\left( 5 \right) = 2000\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\) là số lần giảm \(0,25\$ \). Cước thuê bao hàng tháng lúc này là \(40 - 0,25x\) với \(0 \le x \le 160\) (do mức cước không thể âm), và số thuê bao mới là \(1000x\).
Do đó, tổng số thuê bao là \(100000 + 1000x\).
Hàm doanh thu được cho bởi R = (số thuê bao) x (cước mỗi thuê bao trả)
\[R = \left( {100000 + 1000x} \right)\left( {40 - 0,25x} \right) = 1000\left( {100 + x} \right)\left( {40 - 0,25x} \right) = 1000\left( {4000 + 15x - 0,25{x^2}} \right)\]
Đạo hàm \(R' = 0\), ta được \(R' = 1000\left( {15 - 0,5x} \right) = 0 \Leftrightarrow x = 30.{\rm{ }}\)
Vì tập xác định của \(R\) là khoảng đóng [0; 160] nên \(R\) đạt cực đại tại \(x = 30\) hoặc tại các điểm đầu mút của đoạn [0; 160].
Ta có: \[R\left( 0 \right) = 4000000;\,\,R\left( {30} \right) = 4225000\,;\,\,R\left( {160} \right) = 0\]
Vậy doanh thu tối đa khi \(x = 30\). Điều này tương ứng với 30 lần giảm \(0,25\$ \), tức là cước thuê bao hàng tháng là \(40\$ - 7,5\$ = 32,5\$ \).
Số thuê bao tại mức cước này là \(100000 + 30.\left( {1000} \right) = 130000\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi độ dài đoạn dây gấp tam giác đều là \(x\) thì độ dài đoạn dây gấp hình vuông là \(60 - x\)(mét)
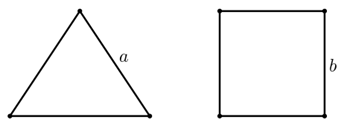
Khi đó \(x = 3a \Leftrightarrow a = \frac{x}{3} \Rightarrow {S_1} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{x^2}\sqrt 3 }}{{36}}\)
Mặt khác: \(60 - x = 4b \Rightarrow b = \frac{{60 - x}}{4} \Rightarrow {S^2} = {b^2} = {\left( {\frac{{60 - x}}{4}} \right)^2}\)
Khi đó \({S_1} + {S_2} = \frac{{{x^2}\sqrt 3 }}{{36}} + {\left( {\frac{{60 - x}}{4}} \right)^2} \Leftrightarrow f\left( x \right) = \frac{{\left( {9 + 4\sqrt 3 } \right){x^2} - 1080x + 32400}}{{144}}\)
Dễ dàng tính được \({\left( {{S_1} + {S_2}} \right)_{\min }} = \min \,f\left( x \right) = f\left( {\frac{{540}}{{9 + 4\sqrt 3 }}} \right) \approx 97,87\,\left( {{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập