Một tam giác đều có cạnh bằng \(2\,{\rm{cm}}\). Độ dài đường tròn ngoại tiếp tam giác đều đó bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
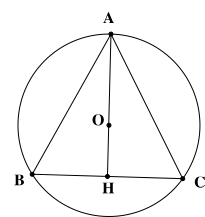
Tâm đường tròn ngoại tiếp tam giác đều trùng với trực tâm và trọng tâm của tam giác đó.
Gọi tam giác \(ABC\) đều có cạnh bằng \(2\,{\rm{cm}}\), tâm đường tròn ngoại tiếp là \(O\).
Kẻ đường cao \(AH\)của tam giác \(ABC\). Tam giác \(AHC\) vuông tại \(H\) có
+) \[AC = 2\,{\rm{cm, HC = }}\frac{1}{2}BC = 1\,{\rm{cm}}\]
+) \(A{H^2} + H{C^2} = A{C^2}\)
\( \Rightarrow A{H^2} + {1^2} = {2^2} \Rightarrow AH = \sqrt 3 \)
\(AO = \frac{2}{3}AH = \frac{{2\sqrt 3 }}{3}\,({\rm{cm}})\)
Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là
\(R = AO = \frac{{2\sqrt 3 }}{3}\,({\rm{cm}})\)
Độ dài đường tròn ngoại tiếp tam giác \(ABC\) là
\(C = 2\pi R = 2\pi \frac{{2\sqrt 3 }}{3} = \frac{{4\pi }}{{\sqrt 3 }}\,\,({\rm{cm}})\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
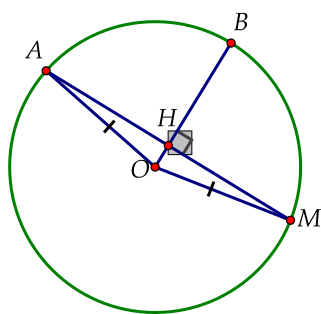
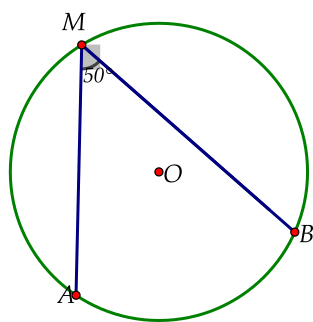
\[\Delta OAM\]cân tại \[O\] \[\left( {OA = OM = R} \right)\].
\[OB \bot AM\]tại \[H\] suy ra \[OB\] đồng thời là đường phân giác của \[\widehat {AOM}\];
\[\widehat {AOB} = \widehat {BOM} = 80^\circ \] \[ \Rightarrow \widehat {AOM} = \widehat {AOB} + \widehat {BOM}\] \[ = 80^\circ + 80^\circ = 160^\circ \].
Do đó số đo của cung nhỏ bằng: \[\widehat {AOM} = 160^\circ \].
Lời giải
Chọn D
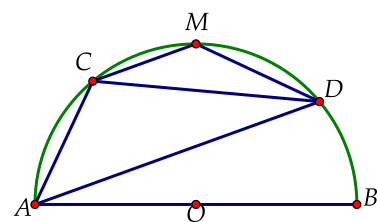
\[M\] là điểm chính giữa của cung \[AB\] nên .
Do \[MC//AD\] nên
\[ \Rightarrow \widehat {COD} = 90^\circ \] (góc ở tâm chắn cung \[CD\])
\[ \Rightarrow \Delta COD\] vuông cân tại \[O \Rightarrow CD = CO\sqrt 2 = R\sqrt 2 \].
Với bài tập này ta cũng có thể lí luận \[ACMD\] là hình thang cân nên \[CD = AM = R\sqrt 2 \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo