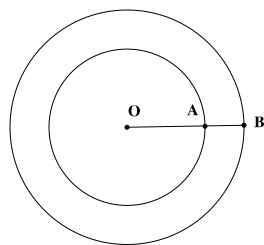
Một vườn hoa hình tròn có bán kính \(OA = 5\,{\rm{m}}\). Ở phía ngoài vườn ta làm một lối đi xung quanh hình vành khăn. Biết diện tích của lối đi bằng diện tích của vườn hoa. Chiều rộng \(AB\) của lối đi xấp xỉ bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Diện tích của mảnh vườn là \(\pi O{A^2}\)
Diện tích của lối đi là \(\pi O{B^2} - \pi O{A^2}\)
Vì diện tích vuòn hoa bằng diện tích lối đi nên
\(\pi O{A^2} = \pi O{B^2} - \pi O{A^2}\) hay \(\pi O{B^2} = 2\pi O{A^2}\) nên \(OB = \sqrt 2 OA\)
Chiều rộng lối đi là
\(AB = OB - OA = \sqrt 2 OA - OA = \sqrt 2 .5 - 5 \approx 2,1\,({\rm{m}})\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
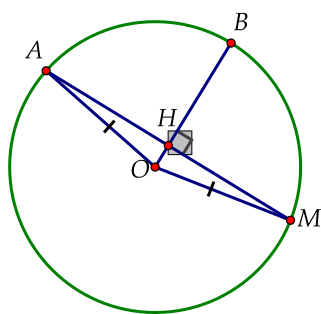
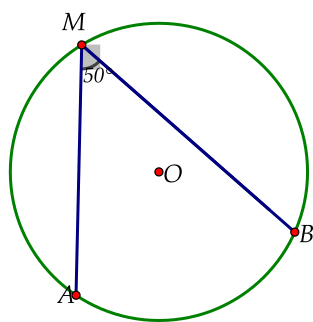
\[\Delta OAM\]cân tại \[O\] \[\left( {OA = OM = R} \right)\].
\[OB \bot AM\]tại \[H\] suy ra \[OB\] đồng thời là đường phân giác của \[\widehat {AOM}\];
\[\widehat {AOB} = \widehat {BOM} = 80^\circ \] \[ \Rightarrow \widehat {AOM} = \widehat {AOB} + \widehat {BOM}\] \[ = 80^\circ + 80^\circ = 160^\circ \].
Do đó số đo của cung nhỏ bằng: \[\widehat {AOM} = 160^\circ \].
Lời giải
Chọn D
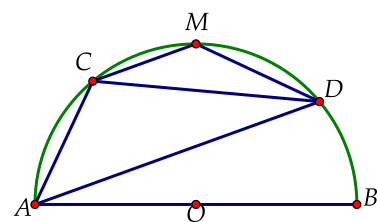
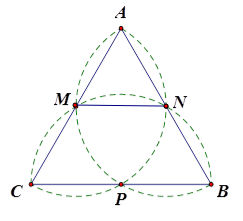
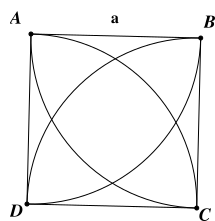
\[M\] là điểm chính giữa của cung \[AB\] nên .
Do \[MC//AD\] nên
\[ \Rightarrow \widehat {COD} = 90^\circ \] (góc ở tâm chắn cung \[CD\])
\[ \Rightarrow \Delta COD\] vuông cân tại \[O \Rightarrow CD = CO\sqrt 2 = R\sqrt 2 \].
Với bài tập này ta cũng có thể lí luận \[ACMD\] là hình thang cân nên \[CD = AM = R\sqrt 2 \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo