Cho \(P = xyz + {x^2}{y^2}{z^2} + {x^3}{y^3}{z^3} + ... + {x^{2020}}{y^{2020}}{z^{2020}}\). Tính giá trị của \(P\) khi biết \(x = 1;y = 1;\)\(z = - 1\).
Quảng cáo
Trả lời:
Lời giải
Đáp án: 0
Ta có: \(P = xyz + {x^2}{y^2}{z^2} + {x^3}{y^3}{z^3} + ... + {x^{2019}}{y^{2019}}{z^{2019}} + {x^{2020}}{y^{2020}}{z^{2020}}\).
Thay \(x = 1;y = 1;z = - 1,\) ta được:
\(P = 1 \cdot 1 \cdot \left( { - 1} \right) + {1^2} \cdot {1^2} \cdot {\left( { - 1} \right)^2} + {1^3}{.1^3}.{\left( { - 1} \right)^3} + ... + {1^{2019}} \cdot {1^{2019}} \cdot {\left( { - 1} \right)^{2019}} + {1^{2020}} \cdot {1^{2020}} \cdot {\left( { - 1} \right)^{2020}}\)
\(P = - 1 + 1 + \left( { - 1} \right) + ... + \left( { - 1} \right) + 1\)
Nhận thấy đa thức \(P\) chứa 2020 hạng tử, trong đó có \(1010\) hạng tử mũ chẵn và \(1010\) hạng tử mũ lẻ.
Do đó, \(P = - 1 + 1 + \left( { - 1} \right) + ... + \left( { - 1} \right) + 1\) có 1010 số hạng \( - 1\) và 1010 số hạng 1.
Suy ra \(P = - 1 + 1 + \left( { - 1} \right) + ... + \left( { - 1} \right) + 1 = - 1 \cdot 1010 + 1 \cdot 1010 = - 1010 + 1010 = 0\).
Vậy với \(x = 1;y = 1;z = - 1\) thì \(P = 0.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Đúng.
Thể tích của bể bơi thứ nhất là: \(1,4 \cdot x \cdot y = 1,4xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Đúng.
Diện tích đáy của bể bơi thứ nhất là: \(x \cdot y = xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Mà diện tích đáy của bê bơi thứ hai gấp 3 lần diện tích đáy của bể bơi thứ nhất.
Do đo, diện tích đáy của bể bơi thứ hai là: \(3xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
c) Sai.
Thể tích của bể bơi thứ hai là: \(1,6 \cdot 3xy = 4,8xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Vì \(4,8 < 5\) nên \(4,8xy < 5xy\).
Do đó, thể tích của bể bơi thứ hai nhỏ hơn \(5xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
d) Đúng.
Tổng thể tích hai bể bơi là: \(4,8xy + 1,4xy = 6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Thể tích nước cần bơm đầy hai bể bơi chính bằng tổng thể tích của của hai bể bơi và bằng \(6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Lời giải
Đáp án đúng là: D
Cách 1.
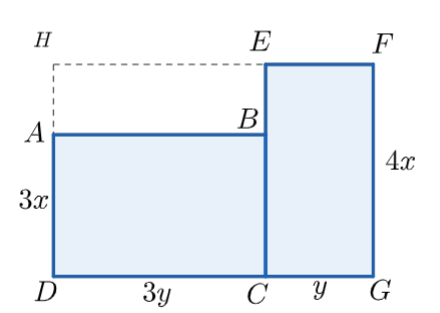
Diện tích phần mảnh đất hình chữ nhật \(ABCD\) là: \(3x \cdot 3y = 9xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích phần mảnh đất hình chữ nhật \(EFGC\) là: \(4x \cdot y = 4xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vậy diện tích phần mảnh đất đã cho là: \(9xy + 4xy = 13xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Cách 2.
Chiều dài của hình chữ nhật \(HFGD\)là: \(3y + y = 4y{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích hình chữ nhật \(HFGD\) là: \(4x \cdot 4y = 16xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Chiều rộng của mảnh đất \(HEBA\) là: \(4x - 3x = x{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích hình chữ nhật \(HEBA\) là: \(x \cdot 3y = 3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích của mảnh đất đã cho là: \(16xy - 3xy = 13xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.