khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

30/09/2025 1,867 Lưu

Phần III. Câu hỏi trắc nghiệm trả lời ngắn (Thí sinh trả lời từ câu 01 đến câu 06)

 Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau

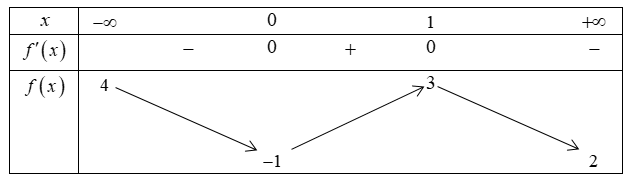
Biết đồ thị hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x}  - x} \right)\) có hai đường tiệm cận ngang là \(y = a\) và \(y = b\), trong đó \(a < b\). Tính \(S = a - 100b\). (ảnh 1)

Biết đồ thị hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x}  - x} \right)\) có hai đường tiệm cận ngang là \(y = a\) và \(y = b\), trong đó \(a < b\). Tính \(S = a - 100b\).

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Đường tiệm cận của đồ thị hàm số lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Ta có \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + 2x}  - x} \right) = 1\) và \(f\left( 1 \right) = 3\), suy ra \(\mathop {\lim }\limits_{x \to  + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to  + \infty } f\left( {\sqrt {{x^2} + 2x}  - x} \right) = 3\).

\(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 2x}  - x} \right) =  + \infty \) và \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 2\), suy ra \(\mathop {\lim }\limits_{x \to  - \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to  - \infty } f\left( {\sqrt {{x^2} + 2x}  - x} \right) = 2\).

Vậy đồ thị hàm số \(g\left( x \right)\) có \(2\) đường tiệm cận ngang \(y = 2\) và \(y = 3\). Suy ra \(a = 2,\,b = 3\).

Suy ra \(S = a - 100b =  - 298\).

Đáp án: \( - 298\)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất \(x\) (sản phẩm) là \(C\left( x \right) = 150x + 900\) (nghìn đồng). Khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm không vượt quá \(t\) (nghìn đồng). Tìm giá trị nhỏ nhất của \(t\).

Lời giải

Chi phí sản xuất trung bình cho mỗi sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{150x + 900}}{x}\).

Ta có \(f'\left( x \right) = \frac{{ - 900}}{{{x^2}}} < 0\,\forall x > 0\).

\(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{150x + 900}}{x} = 150\).

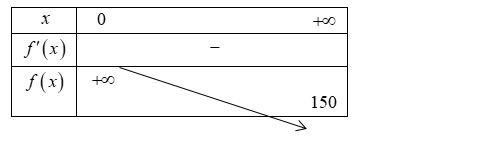
Tìm giá trị nhỏ nhất của t . (ảnh 1)

Vậy khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm càng giảm, nhưng không dưới \(150\) nghìn đồng.

Đáp án: \(150\)

Câu 2

Đường thẳng \(y = ax + b\) (\(a \ne 0\)) là đường tiệm cận xiên của đồ thị hàm số \(y = f(x)\) nếu:
A. \(\mathop {\lim }\limits_{x \to a} \left[ {f(x) - (ax + b)} \right] = 0\).                 
B. \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = a\).
C. \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\)             
D. \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = b\).

Lời giải

Chọn C

Theo định nghĩa của tiệm cận xiên.

Câu 3

Đồ thị hàm số \(y = \sqrt {{x^2} + 2x + 2} \) có mấy đường tiệm cận xiên:
A. \(0\).                       
B. \(1\).                     
C. \(2\).                           
D. \(3\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số \(y = \frac{{ - {x^2} + 4x + 3 + m}}{{x - 2}}\) \[\left( C \right)\].

a) Khi \(m = 0\), tiệm cận đứng của hàm số là \(x = 2\).

b) Khi \(m = 0\), tọa độ giao điểm của tiệm cận đứng đồ thị và đường thẳng \(x - y - 1 = 0\) thuộc parabol: \(y = {x^2}\)

c) Khi \(m = 0\), lấy \(M\) là điểm bất kỳ trên đồ thị \(\left( C \right)\), gọi \({d_1}\) là khoảng cách từ M đến đường tiệm cận tiệm cận đứng, gọi \({d_2}\) là khoảng cách từ M đến đường thẳng \(y =  - x + 2\,\). Tích \({d_1}.{d_2} = 7\)

d) Gọi S là tập hợp các giá trị nguyên dương của m để hàm số không có tiệm cận đứng. Số phần tử của S là 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số \[y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\] \[\left( {a \ne 0} \right)\]có đồ thị như hình vẽ bên dưới

Tìm số đường tiệm cận đứng của đồ thị hàm số \(g\left( x \right) = \frac{{\sqrt x }}{{f\left( {{x^2} - 1} \right) - 4}}\). (ảnh 1)

Tìm số đường tiệm cận đứng của đồ thị hàm số \(g\left( x \right) = \frac{{\sqrt x }}{{f\left( {{x^2} - 1} \right) - 4}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

PHẦN I: Câu trắc nghiệm nhiều phương án lựa chonl. Thí sinh trả lời từ câu 1 đến câu 12 Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \).
A. Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng \(x = 2\).
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho không có tiệm cận ngang

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập